Definition of Resolution for First-Order Logic
This is the definition of resolution rule for first-order logic clauses.
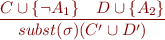
where  ,
,  are renamings,
are renamings, 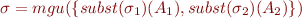 ,
where
,
where  and
and  .
.
We will call the above rule mgu-resolution if we need to differentiate it from instantiation followed by resolution.