Substitutions for First-Order Logic
Motivating Example
It is important to be precise about substitutions in first-order logic. For example, we would like to derive from formula 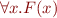 formula
formula 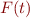 , denoted
, denoted 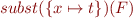 that results from substituting a term
that results from substituting a term  instead of
instead of  . For example, from
. For example, from  we would like to derive
we would like to derive 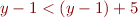 . Consider, however formula
. Consider, however formula
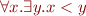
Consider an interpretation in integers. This formula is true in this domain. Now substitute instead of x the term y+1. We obtain

This formula is false. We say that the variable  in term
in term  was captured during substitution. When doing substitution in first-order logic we must avoid variable capture. One way to do this is to rename bound variables. Suppose we want to instantiate the formula
was captured during substitution. When doing substitution in first-order logic we must avoid variable capture. One way to do this is to rename bound variables. Suppose we want to instantiate the formula 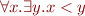 with
with  . Then we first rename variables in the formula, obtaining
. Then we first rename variables in the formula, obtaining
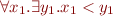
and then after substitution 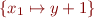 we obtain
we obtain  , which is a correct consequence of
, which is a correct consequence of 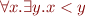 .
.
Naive and Safe Substitutions
Let  be a set of variables (that is,
be a set of variables (that is,  ). A variable substitution is a function
). A variable substitution is a function  where
where  is the set of terms first-order logic.
is the set of terms first-order logic.
We define naive substitution recursively, first for terms:
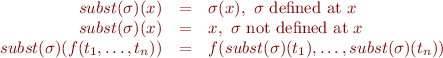
and then for formulas:
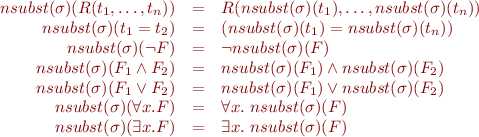
Lemma: Let 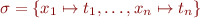 be a variable substitution and
be a variable substitution and  a term. Then for every interpretation
a term. Then for every interpretation  ,
,
![Equation \begin{equation*}
e_T(nsubst(\sigma)(t))(I) = e_T(t)(I[x_1 \mapsto e_T(t_1)(I),\ldots, x_n \mapsto e_T(t_n)(I)])
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imgaada7d65b5fea6a6388c76f6a346c5c1.png)
To avoid variable capture, we introduce in addition to  a safe substitution,
a safe substitution, 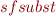 .
.
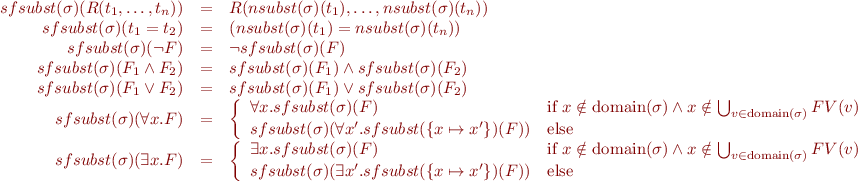
Lemma: Let 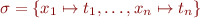 be a variable substitution and
be a variable substitution and  a term. Then for every interpretation
a term. Then for every interpretation  ,
,
![Equation \begin{equation*}
e_F(sfsubst(\sigma)(F))(I) = e_F(F)(I[x_1 \mapsto e_T(t_1)(I),\ldots, x_n \mapsto e_T(t_n)(I)])
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img6ea9615b95a35ebbe1725d60a42a3bfc.png)
Lemma: 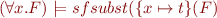 .
.