Substitution Theorems for Propositional Logic
Relate syntax and semantics.
Called metatheorems, because they are not formulas within the logic, but formulas about the logic.
From semantics we can prove the following lemma by induction.
Lemma: if 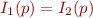 for every
for every 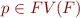 , then
, then 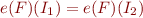 .
.
Substitutions
Substitution is a maping formulas to formulas,
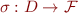
where 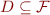 is the domain of substitution, usually finite. We write it
is the domain of substitution, usually finite. We write it
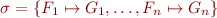
Let  be set of all substitutions.
be set of all substitutions.
Substitution operator subst takes such a map and a formula and returns a new formula.
Recursive definition of subst:
For 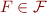 we write
we write  instead of
instead of 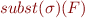 , so
, so

Variable substitution is substitution where the domain is a subset of  - it only replaces variables, not complex formulas.
- it only replaces variables, not complex formulas.
Theorem: For formula  , interpretation
, interpretation  and variable substitution
and variable substitution 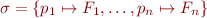 ,
,
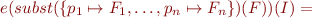
Corollary (tautology instances): if 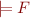 , then
, then 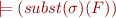 for every variable substitution
for every variable substitution  .
.
We say that two formulas are equivalent if  .
.
Lemma: If  then for every interpretation
then for every interpretation  we have
we have 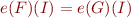 .
.
From the tautology instances Corrolary we obtain.
Corollary: if  and
and  is a variable substitution, then
is a variable substitution, then  .
.
Does the theorem hold if  is not a variable substitution?
is not a variable substitution?
This theorem was about transforming formulas from the outside, ignoring the structure of certain subformulas.
We next justify transforming formulas from inside.
We say that 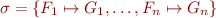 is equivalence-preserving iff for all
is equivalence-preserving iff for all  where
where 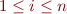 we have
we have 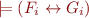 .
.
Theorem on Substituting Equivalent Subformulas: if  is equivalence-preserving, then for every formula
is equivalence-preserving, then for every formula  we have
we have 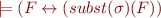 .
.
![Equation \begin{equation*}
e(F)(I[p_1 \mapsto e(F_1)(I),\ldots,p_n \mapsto e(F_n)(I)])
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imga7b5f8e99840e1a8fa1e9db3a5f15828.png)