A Congruence Closure Theorem
Recall that we convert all relation symbols into function symbols (to simplify the Axioms for Equality).
Theorem Let  be a set of ground equalities and disequalities
(
be a set of ground equalities and disequalities
(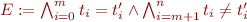 ).
Then the following are equivalent:
).
Then the following are equivalent:
 is satisfiable
is satisfiable- there exists a congruence on ground terms in which
 is true
is true  is true in the least congruence
is true in the least congruence  containing
containing 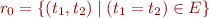
- for the least congruence
 containing
containing 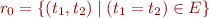 we have
we have 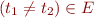 implies
implies 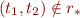
Proof:
The equivalence of first two statements
The equivalence of last two statements follows by definition.
We show equivalence of second and third statement.
Third statement trivially implies second.
Consider any congruence  in which
in which  is true.
is true.
Proof End.
 .
. .
.