Axioms for Equality
The following definitions are useful when axiomatizing equality in a logic that does not have equality built in. It is also useful when discussing algorithms that automate reasoning about equality.
For language  and a relation symbol
and a relation symbol  , the theory of equality, denoted AxEq, is the following set of formulas:
, the theory of equality, denoted AxEq, is the following set of formulas:
Definition: if an interpretation  the axioms
the axioms  are true, then we call
are true, then we call 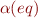 (the interpretation of eq) a congruence relation for interpretation
(the interpretation of eq) a congruence relation for interpretation  .
.
Side remark: Functions are relations. However, the condition above for function symbols is weaker than the condition for relation symbols. If  is a function, then the relation
is a function, then the relation 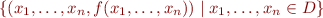 does not satisfy the congruence condition because it only has one result, namely
does not satisfy the congruence condition because it only has one result, namely 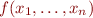 , and not all the results that are in relation eq with
, and not all the results that are in relation eq with 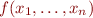 . However, if we start from the condition for functions and treat relations as functions that return true or false, we obtain the condition for relations. So, it makes sense here to treat relations as a special case of functions.
. However, if we start from the condition for functions and treat relations as functions that return true or false, we obtain the condition for relations. So, it makes sense here to treat relations as a special case of functions.
References
- Calculus of Computation Textbook, Section 3.1
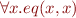
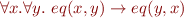
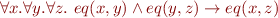
 function symbol with
function symbol with 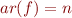 ,
, 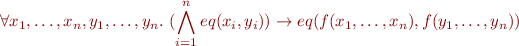
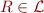 relation symbol with
relation symbol with 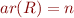 ,
,