LARA

Vepar

Vepar stands for Verification, Proof and Automated Reasoning.

The name is meant to be dangerous, whether you fear ghosts or wild hogs.

Vepar hopes to be a Grand Unified Reasoning Utility, but it is not GURU

Vepar HOL

Vepar Set Theory

Vepar Numbers Hierarchy

Soft Typing

Working Pages

MONA HOL

functional

Topics to Discuss Later

  • unicode use
  • import declarations

SVN repository

https://larasvn.epfl.ch/svn-repos/projects/guru/trunk

Algorithmic Questions

Can we have general constraint propagation rules, and even derive new constraint propagation rules from lemmas that are shown correct?

This can build on Philippe's experience with NC(T).

Solving Non-clausal Formulas with DPLL search

Ideas:

  • using lemmas as propagation rules (basically, if we identify that R(x0,y) implies y=f(x0) under certain condition where f is computable)
  • preserving executable programs and turning them into very efficient constraint propagation rules (see delayed choice and symbolic execution, logic programming, and using ACL2 for symbolic execution)
  • doing static analysis on formulas to identify propagation rules?

Getting Things to Work

  • parsing for:
  • if p then q else r, let (x::T) = e in f
  • parsing set comprehensions (lhs has only variable or pair of variables) and finite sets, pairs, transitive closure
  • all the time keep pretty printer up-to-date and check that if it works with formDecier and Isabelle
  • develop pretty printer to SMT format
  • no bitvectors for now
  • fast bottom-up type inference (if all variables have types given at their binders)

Type Inference and Isabelle Input

  • a separate parser not just lambda expressions, but parsing of infix &,|,–>, and ALL,EX,…
  • perhaps an Earley parser, or LALR(1), or Packrat

Scala Syntax and Semantics

  • define Pure Scala (see proposal for Sinergia)
    • representing quantifiers, sets, lists
  • parse Pure Scala
  • emit Pure Scala so it can be run

Sets

  • basic set operations membership, (union, intersection, difference) and comprehensions (Collect)

Bitvectors

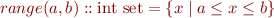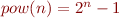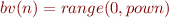Define constant $range(a,b) :: \mbox{int}\ \mbox{set} = \{ x \mid a \le x \le b \}$, $pow(n)=2^n-1$, and $bv(n) = range(0,pow n)$, so users can write

\begin{equation*} \begin{array}{l} \forall x \in bv(n). \forall y \in bv(n). x + y = y + x \\ \forall x \in bv(n). \exists y \in bv(n).\ x (\mbox{bvplus}\ (pow\ n)) y = 0 \end{array} \end{equation*}

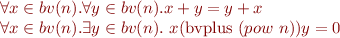
Multisets

  • syntax and decision procedures for them

Fixpoints

Fixpoints can be used to define recursive types, recursive functions, etc. Actual recursive definitions can be syntactic sugar for appropriate fixpoint expressions.

Because we are typically finding with simple functions, it seems sufficient to consider operator that computed

\begin{equation*} \bigsqcup_i F^i(\bot) \end{equation*}

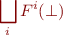
if it is given:

  • function $F$
  • bottom element $\bot$ belonging to set $A$
  • least upper bound function $2^A \to A$

About

(originally repoduced from doc/about.txt on the SVN.. now overrides this file).

A tool for proving formulas in an expressive logic by combining a wide range of reasoning techniques.

formDecider from Jahob is a predecessor of Guru, but Guru will be a fully redesigned version.

Logical basis: classical higher order logic.

Types:

  • bool
  • int /* unbounded */, nat /* do we need it - make it subset */
  • bitvector-k (check what CVC3 does)
  • real /* mathematical R - continuous integers that include \pi */
  • char

Constructors:

  • 'a ⇒ 'b
  • 'a set (isomorphic to 'a ⇒ bool)
  • 'a multiset (isomorphic to 'a ⇒ nat)
  • 'a list
  • 'a * 'b

For algebraic data types, perhaps look at a subset of Isabelle theories and have datatype declarations introduced exactly as in Isabelle.

e.g. 

datatype 'a Tree = Nil | Node ("'a Tree") 'a ("'a Tree")

where 'a is type parameter

Follows syntax and semantics of Isabelle/HOL whenever possible. However, the semantics is built-in as opposed to axiomatically developed.

See also formula definition in 

jahob/src/form/form.ml

Validation, e.g. go to jahob/examples/sorting/insertionsort and run 

../../../bin/jahob.opt -nobackground -method Insertion.insertionSort Insertion.java -v -usedp z3

or 

../../../bin/jahob.opt -nobackground -method Insertion.insertionSort Insertion.java -usedp isa:TimeOut=0

and then see the *.thy* files in /tmp

Consider connections with:

Good exposition of classical higher-order logic is in section 51 of

@Book{Andrews02IntroductionMathematicalLogicTypeTheory, 

author =       {Peter B. Andrews},
title =        {An Introduction to Mathematical Logic and Type Theory: To Truth Through Proof},
publisher =    {Springer (Kluwer)},
year =         2002,
edition = {2nd},
isbn = {ISBN 1402007639}

}

Tasks

(originally repoduced from doc/tasks.txt on the SVN.. now overrides this file).

  • Define syntax and semantics: all on top of lambda calculus. Implement as ASTs in Scala.
  • Settle for some concrete syntax(es)
    • Pure Scala
    • Isabelle/HOL
    • SMT++
  • Choose a parsing approach, implement parser
 jahob/src/form/yaccForm.mly - yacc
 jahob/src/form/lexForm.mll - lex
  • printer to STP
  jahob/src/smtlib/
  • printer to Isabelle: 
 jahob/src/form/printForm.ml
  • evaluator on finite models and/or int32 ?
  • what to do about overloading?
  • Identify sublanguage for translation to SMT, specifically
    • STP
    • Z3
    • CVC3
  • Identify sublanguage for translation to multisets
  • Implement multiset decision procedure
  • DPLL engine, congruence closure
  • Algebraic data types
  • Integer solver as done by Ruzica
  • someone? connection to Alloy and Kodkod

Initial source of examples:

More fun ideas

  • Apply DPLL-like search to programs
    • use evaluation of expressions as a mean to do “constraint propagation” (interpretation is just CP, when you think about it)
    • evaluation of integers is not restricted to linear arithmetic, for instance.

References

Related Research Proposals - Not for Distribution