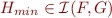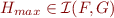Interpolation
Interpolation is one of the main methods to find predicates in predicate abstraction, and, more generally, to perform counterexample-based refinement of abstractions.
Definition of Interpolant:
Given two formulas  and
and  , such that
, such that 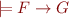 , an interpolant for
, an interpolant for 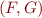 is a formula
is a formula  such that:
such that:
1) 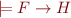
2) 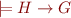
3) 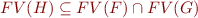
Paper on Interpolation in Verification
Here are two simple ways to construct an interpolant:
- We can quantify existentially all variables in
 that are not in
that are not in  .
.
 where
where 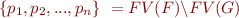
- We can quantify universally all variables in
 that are not in
that are not in  .
.
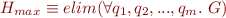 where
where 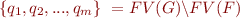
Definition: 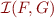 denote the set of all interpolants for
denote the set of all interpolants for 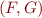 , that is,
, that is,

Theorem: The following properties hold for  ,
,  ,
, 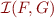 defined above:
defined above:
We have observed before that, if a theory has quantifier elimination, then it also has interpolants.
Therefore, all theories in the List of Theories Admitting QE have interpolants. (But interpolants may exist even if there is no quantifier elimination.)
Interpolants from Resolution Proofs
Interpolants in resolution: instead of validity of implication, we look at unsatisfiability.
Let  ,
,  be sets of clauses such that
be sets of clauses such that 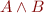 is not satisfiable. An interpolant is a formula
is not satisfiable. An interpolant is a formula  such that
such that
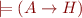 and
and 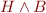 is not satisfiable and
is not satisfiable and 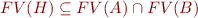
Construct resolution tree that derives a contradiction from  . The tree has elements of
. The tree has elements of  as leaves and results of application of resolution as nodes. For each clause
as leaves and results of application of resolution as nodes. For each clause  in resolution tree we define recursively formula
in resolution tree we define recursively formula  and show that
and show that  is interpolant for these two formulas:
is interpolant for these two formulas:
where  denotes the conjunction of those literals from
denotes the conjunction of those literals from  whose propositional variables belong to
whose propositional variables belong to 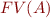 , similarly for
, similarly for  .
.
It follows that for empty clause the 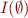 is the interpolant for
is the interpolant for 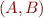 .
.
Construction of  :
:
- if
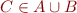 then
then- if
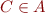 then
then 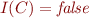
- if
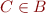 then
then 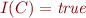
- if
 is result of applying resolution to
is result of applying resolution to  ,
,  along propositional variable
along propositional variable  where
where  , and
, and 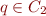 , then
, then- if
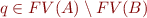 then
then 
- if
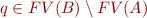 then
then 
- if
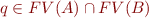 then
then 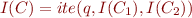
We prove that  has the desired property by induction on the structure of the resolution proof tree.
has the desired property by induction on the structure of the resolution proof tree.
More information in e.g.