Vepar HOL

Vepar's core logic is classical higher-order logic (HOL).

It is used as a 'meta logic' in the sense that most constructs are not described directly using their HOL definitions, but rather within the Vepar Set Theory defined inside it.

We give abstract syntax using context-free grammars and introduce the specific terminology we use.

Vepar HOL tries to follow Isabelle syntax as closely as possible.

HOL Types

Simply typed lambda calculus with built in types 'prop' (for propositions) and 'set' (for sets from Vepar Set Theory).

Functions can be built using standard function arrow constructor. However, this is primarily used to build up the system and introduce shorthands, most user-defined functions are functions in set-theoretic sets functions and thus defined in Vepar Set Theory.

Abstract:

t ::= Set | Prop | Arrow(t,t) | \alpha

Concrete:

$\begin{equation*} t ::= \textsf{set} \mid \textsf{prop} \mid \alpha \mid (t \Rightarrow t) \end{equation*}$

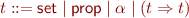
Terms

Abstract:

f ::= (Var,t) | (App(f,f),t) | (Lambda(i,f),t)
Var ::= Index(Int) | Name(String)

Concrete:

$\begin{equation*} f ::= (v::t) \mid ((f\ f)::t) \mid ((\% (v::t).\ f)::t) \end{equation*}$

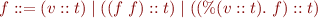
Notes:

terms are represented as de Bruijn indices but store variable names for printing purposes.

Standard HOL Constants and Definitions

We introduce here the standard HOL definitions, explaining the part of the context not specific to Vepar Set Theory.

polymorphic:

ALL :: (a => prop) => prop
EX  :: (a => prop) => prop
=   :: a => a => prop
let x=E in F  === (% x.F)E
if ... then ... else :: (prop => a => a => a)
epsilon :: (a => prop) => prop

monomorphic:

&
|
~
-->