Context-Free Grammars

Purpose and Expressive Power

A context-free grammar is a way to specify languages.

Context-free grammars are more powerful than regular expressions: for each regular expression there is an equivalent context-free grammar, but the converse need not hold. Context-free grammars supposed not just iteration like regular expressions, but also more general forms of recursion.

ab Example

Strings of the form 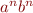$a^n b^n$ for $n \ge 1$ can be described by this recursive grammar

S ::= "ab" | "a" S "b"

This language is not regular.

Definition

Definition: Context-free grammar consists of

set of terminal symbols (letters of the alphabet)
set of non-terminal symbols (used to recursively define sets of strings)
one of the non-terminal symbols that is designed to be the starting non-terminal
a finite set of productions, which are grammar rules of the form

N ::= s1 ... sn

where N is a non-terminal, and each s1,…,sn is either a terminal or a non-terminal. The sequence s1…sn can be empty.

A string of terminals is generated by a grammar iff we can obtain this string by transforming sequences of terminals and non-terminals as follows:

the initial string contains only starting non-terminal
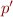at each step, we select a non-terminal N in our string $p$ and select a production with N as left-hand side, and replace non-terminal with the right-hand side, obtaining string $p'$ (this process is denoted $p \Rightarrow p'$ )

$u \Rightarrow^{+} v$ means $v$ is obtained from $u$ by one or more $\Rightarrow$ steps

$u \Rightarrow^{*} v$ means $v$ is obtained from $u$ by zero or more $\Rightarrow$ steps

$\begin{equation*} L(G) = \{ w \mid w \in \Sigma^*, \ S \Rightarrow^* w \} \end{equation*}$

Shorthands for Writing Context-Free Grammars

Note: we group multiple productions with same left-hand side, writing

N -> p | q

instead of

N -> p
N -> q

Also, we allow nesting, writing e.g.

N -> p (q | r) s

instead of

N -> p M s
M -> q | r

Finally, we allow the use of star as in regular expressions, because

N -> p*

is the same as

N -> "" | p N

Example of generating string aaabbb:

S -> aSb -> aaSbb -> aaabbb

Example: Polynomials

Polynomials are expressions that use variables, constants, operators +, * and parentheses. We can describe strings representing polynomials as follows:

polynomial ::= term | term "+" polynomial
term ::= factor | factor "*" term
factor ::= constant | variable | "(" polynomial ")"

we can also describe variables and constants:

variable ::= letter | variable digitSequence
constant ::= digitSequence | "-" digitSequence
digitSequence ::= digit | digit digitSequence
digit ::= "0" | "1" | "2" | ... | "9"
letter ::= "a" | "b" | "c" | ... | "x" | "y" | "z"

Example of generating x+3*y:

(Each table entry represents one step in relation $\Rightarrow$ .)

Example: English Sentences

This generates certain simple English sentences.

Sentence = Simple | Belief
Simple = Person liking Person
liking = "likes" | "does" "not" "like"
Person = "Barack" | "Joe" | "John" | "Sarah" | "Snoopy"
Belief = Person believing "that" Sentence optBut
believing = "believes" | "does" "not" "believe"
optBut = "" | "," "but" Sentence

Example sentence generated by above grammar:

“John does not believe that Barack believes that Sarah likes Snoopy, but Snoopy believes that Barack likes Joe.”

examples of using grammars for text generation
type “compiler construction” into http://www.essaygenerator.com

“How much responsibility lies with compiler construction? We can say that compiler construction deserves all of the attention it gets. It establishes order, provides financial security and it brings the best out in people.”

LARA