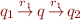Equivalence of finite state machines and regular expression languages
We next show that a language is given by a regular expression if and only if it is a language of some finite state machine.
If a language is given by one of these two ways, we can always convert to the other if this is more convenient.
- regular expressions can be easier to specify textually
- it is easier to check whether a string is accepted by a finite state machine
Every language given by a regular expression is accepted by some finite state machine
By induction on the structure of regular expressions, we construct the finite state machine that accepts this language.
For the base case, observe that we can easily construct finite state machines for empty language  , and a finite state machine for a singleton language
, and a finite state machine for a singleton language  for
for  .
.
For the inductive step, we use closure properties of finite state machines for the cases of union, concatenation, and iteration.
Every language accepted by a finite state machine is given by some regular expression
Finite state machines with regular expression labels. We first generalize the notion of a finite state automaton so that we can label its edges not only with elements of  as in the standard definition of finite state machine and with epsilon transitions as in finite state machine with epsilon transitions, but with arbitrary regular expressions.
as in the standard definition of finite state machine and with epsilon transitions as in finite state machine with epsilon transitions, but with arbitrary regular expressions.
An accepting execution for such a generalized finite state machine is a sequence of states and regular expressions 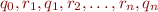 with
with  , and the accepted strings of that execution are all strings in the union of
, and the accepted strings of that execution are all strings in the union of 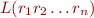 over all such accepting sequences.
over all such accepting sequences.
Note that if all regular expressions are elements of  , the definition reduces to the standard definition of finite state machine.
, the definition reduces to the standard definition of finite state machine.
Preparing for conversion to regular expression. To convert a finite state machine into a regular expression, we first view it as a generalized finite state machine, and then eliminate states of the state machine one by one. We start the process by creating a fresh initial state 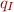 and fresh final state
and fresh final state 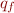 and expressing all final states in
and expressing all final states in  by
by  transitions to
transitions to 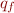 . We let
. We let 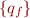 be the new set of final states. For any pair of states, we then ensure that there is exactly one edge between them:
be the new set of final states. For any pair of states, we then ensure that there is exactly one edge between them:
- if there was no edge, we introduce an edge with the label is
 ;
; - if there are multiple edges with labels
 , we introduce instead one edge whose label is the regular expression
, we introduce instead one edge whose label is the regular expression 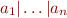 .
.
Elimination step: We show how to eliminate a state  (we assume
(we assume  is not initial and not a final state).
is not initial and not a final state).
- let the self-loop edge labelled
 be
be 
- for every two states
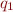 and
and  (possibly equal), distinct from
(possibly equal), distinct from  :
: - suppose we have these regular expressions on edges:
- extend label from
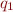 to
to  with
with 
At the end, we are left with one non-empty edge from  to
to 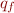 , whose label is the desired regular expression.
, whose label is the desired regular expression.
Some consequences
- Given an automaton that accepts
 , construct an automaton that accepts
, construct an automaton that accepts  ?
? - Given a regular expression for
 , construct a regular expression for
, construct a regular expression for  ?
? - Given two regular expressions, how to compute their intersection?
Exercise
Consider alphabet 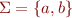 . A string
. A string  is desperate if it contains 'aaa' as a substring. Construct a regular expression that describes the set of all strings that are not desperate.
is desperate if it contains 'aaa' as a substring. Construct a regular expression that describes the set of all strings that are not desperate.