Closure properties of finite state machines
If we have some number of finite state machines, we show how to create a finite state machine whose language is union, intersection, complement, concatenation, or iteration of the languages of these state machines.
Complement
Let 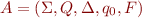 . Let
. Let 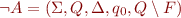 . Then
. Then 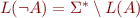 .
.
This is only true if A is a deterministic FSM. If A is nondeterministic, we must first convert it into an equivalent deterministic FSM, then take the complement. This can result in an exponential blowup of the number of states.
Union
Put two machines together disjointly, with a new initial state that has epsilon transitions to the original initial states.
Let 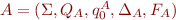 and
and 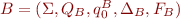 .
.
Then the union of the two automata will be 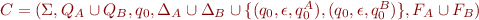 .
.
Intersection
Product of state spaces, even for non-deterministic machines.
Concatenation
Put one machine after another, with epsilon transitions from the accepting states of the first machine to the start state of the second machine.
The new accepting states are those of the second machine.
Iteration (Kleene star)
Create a new initial state which is accepting and has an epsilon transition to the old start state.
Put a loop around the existing machine by adding epsilon transitions from the accepting states to the new start state.
Comments
If we start with deterministic machines, for which of the above constructions will we get a deterministic machine as a result?
What is the cost of computing the machine for the complement of the language?