Finite state machine with epsilon transitions

Definition

Finite state machine with epsilon transitions is an extension of a finite state machine where transitions can be labelled by $\epsilon$ . If such a transition 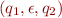$(q_1,\epsilon,q_2)$ exists then an automaton may transition from 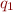$q_1$ to $q_2$ without consuming any portion of the input string.

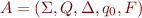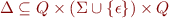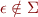As for finite state machine, we define a finite state machine with epsilon transitions as a 5-tuple $A = (\Sigma,Q,\Delta,q_0,F)$ with the only difference that $\Delta \subseteq Q \times (\Sigma \cup \{\epsilon\}) \times Q$ where $\epsilon \notin \Sigma$ is a special symbol.

Execution of machine with epsilon transitions

An execution is now an alternating sequence of states and elements of 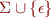$\Sigma \cup \{\epsilon\}$ . As before, an accepting execution starts from initial state and its last item is a final state. The word accepted by a given accepting execution is given by concatenating the labels of all transitions in an execution, with $\epsilon$ transitions ignored.

Note: we could further generalize to allow arbitrary strings

Eliminating epsilon transitions

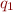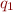Epsilon transitions are a matter of convenience and can always be eliminated by the following process. For each state $q_1 \in Q$ we compute the set of all states $q_2$ reachable from $q_1$ along the edges with $\epsilon$ transitions. We then add the outgoing non-epsilon edges of all such $q_2$ to the existing outgoing edges of $q_1$ . We also insert 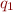$q_1$ into $F$ whenever one of the states $q_2$ is in $F$ . The resulting automaton accepts the same langauge and has no $\epsilon$ transitions.