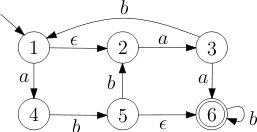
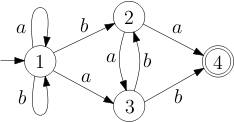
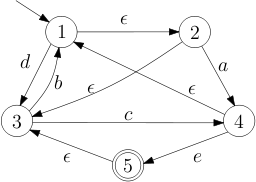
Exercises 01
Exercise 1
Assume the following extensions to the regular expressions. In each case describe why the modification does not actually change the expressibility.
- The intersection of two regular expressions.
- The optional expression
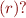 denoting that expression
denoting that expression  optional
optional - Limiting Kleene repetition with a maximum and minimum bound
Design your own operator that extends regular expressions to make it possible to express nested comments.
Exercise 2
Exercise 3
Integer literals are in three forms in Scala: decimal, hexadecimal and octal. The compiler discriminates different classes from their beginning. Decimal integers are started with a non-zero digit. Hexadecimal numbers begin with 0x or 0X and may contain the digits from 0 through 9 as well as upper or lowercase digits A to F afterwards. If the integer number starts with zero, it is in octal representation so it can contain only digits 0 through 7. There can be an l or L at the end of the literal to show the number is Long.
- Draw a single DFA that accepts all the allowable integer literals.
- Write the corresponding regular expression.
Exercise 4
Design a DFA which accepts all the binary numbers divisible by 6. For example your automaton should accept the words 0, 110 (6 decimal) and 10010 (18 decimal).
Exercise 5
Let  be the language of strings on
be the language of strings on 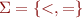 defined by
defined by 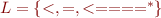 that is,
that is,  .
.
- Construct a DFA that accepts
 .
. - Describe how the lexical analyzer will tokenize the following inputs.
- <=====
- ==<==<==<==<==
- <=====<
Exercise 6
For each of the following languages find the first set. Determine if the language is nullable.
(a|b)*(b|d)((c|a|d)* | a*)
Exercise 7
Recall the maximal munch rule: lexical analyzer should eagerly accept the longest token that it can recognize from the current point.
- Consider the following specification of tokens, the numbers in parentheses gives the name of the token given by the regular expression.
(1) a(ab)* (2) b*(ac)* (3) cba (4) c+
Use the maximal munch rule to tokenize the following strings according to the specification
- c a c c a b a c a c c b a b c
- c c c a a b a b a c c b a b c c b a b a c
- If we do not use the maximal munch rule, is another tokenization possible?
- Give an example of a regular expression and an input string, where the regular expression is able to split the input strings into tokens, but it is unable to do so if we use the maximal munch rule.