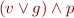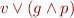About Parsing Potentially Ambiguous Context-Free Grammars
Given a context-free grammar  , how to check if
, how to check if 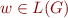 ?
?
- recursive descent gives efficient answer when
 is LL(1)
is LL(1) - we now see how to do it for arbitrary context-free grammar

Applications:
- applications in Natural Language Processing
- parsing mathematical formulas: e.g. the parser within the Isabelle interactive theorem prover
- more flexibility in writing the grammar for programming languages
Example from Natural Language Processing:
A student gets a good recommendation letter if the student makes a good impression on Viktor or makes a good impression on Giuliano and does an excellent project.
Interpretation on the condition for good recommendation letter:
In program natural language processing we need to represent multiple possible interpretations and resolve them using other methods (probabilities derived from a training set, or semantic interpretation using automated reasoning tools in some semantic domain).
Example from parsing formulas:: The Isabelle interactive theorem prover supports higher-order logic, which contains typed lambda calculus and first-order logic. The theorem prover has a flexible syntax that allows writing expressions close to the common mathematical practice. for example
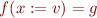
makes  denote the function such that
denote the function such that 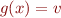 and
and 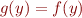 for
for 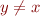 . Unfortunatelly, the above expression looks like application of function
. Unfortunatelly, the above expression looks like application of function  to some value of the form
to some value of the form  , so it can be difficult to parse. Another example in Isabelle are expressions denoting sets. The formula
, so it can be difficult to parse. Another example in Isabelle are expressions denoting sets. The formula
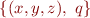
denotes a singleton set containing two elements: the first element is a triple 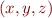 , the second element is
, the second element is  . On the other hand, the expression
. On the other hand, the expression
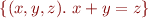
is a set comprehension denoting infinitely many elements. These two expressions can also be difficult to differentiate in simple parsers.