Please hand in your exercises before Wednesday, Oct. 22nd, 8.15am.

Consider the following grammar:

S' → S $

S → s

S → { S2 }

S → i c S

S → i c S e S

S2 → S2 S | S

1. Parse the following string: “icicse{ss}$” using Earley parsing (show the list of sets of items you get until the string is recognized).
2. How many parses did you get?
3. Which part of a programming language grammar would typically look like this? How would the ambiguity be resolved?

Consider the following grammar:

S' → S $

S → S + S

S → x

…and the familiy of strings sum(n)$, where:

• sum(0) = “x”
• sum(1) = “x+x”
• sum(2) = “x+x+x”
• …
• sum(n) = sum(n-1) “+x”

1. Assume you are applying Earley parsing on these strings. Give an expression of the number of items in each state 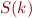in terms of . Argue that, except for the last state, this does not depend on which string sum(n)$ you are parsing.
2. Based on the states you are getting, give an expression in terms of n of the number of parses for each string sum(n)$.

edit: A good explanation for the second point was given as exercise here (ex 4). The detailed correction is available here (in French, I'm afraid).