Insertion into Doubly-Linked List

(Figure of doubly-linked list of size 3.)

Code:

   assume P;
   if (first == null) {
     first = n;
     n.next = null;
     n.prev = null;
   } else {
     n.next = first;
     first.prev = n;
     n.prev = null;
     first = n;
   }
   assert Q;

Where $P$ is

$\begin{equation*}\begin{array}{l} n \neq null\ \land \\ next(n) = null \land prev(n)=null\ \land \\ prev(first) = null\ \land \ Q \end{array} \end{equation*}$

and where $Q$ is

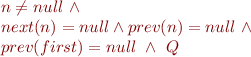
$\begin{equation*}\begin{array}{l} \forall x.\forall y. prev(x)=y\ \ \rightarrow \\ \qquad (y \neq null \rightarrow next(y)=x)\ \land \\ \qquad (y = null \land x \neq null \rightarrow (\forall z. next(z) \neq x)) \end{array}\end{equation*}$

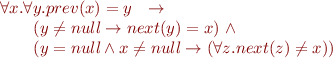
Corresponding Jahob file (call it dll-example.java).

We can check the add method by:

jahob.opt dll-example.java -method Simple.add -usedp cvcl

How can we build a verification conditions for such programs?

we need to be able to reason about data structures (objects, references, arrays)

Illustration of phases in Jahob system when loop invariants are specified:

source code
syntax tree
jast: simplified statements (use option -jast to see it)
ast: guarded commands with loops (use option -ast to see it)
sast (use option -sast to see it):
- eliminating loops with loop invariants by translation to guarded commands (as in Backward VCG with Loops)
- incorporate preconditions and postconditions using assume and assert
compute weakest precondition with respect to 'true' - this is verification condition (VC)
simplify VC, split into multiple formulas, eliminate easily provable formulas
- use -v to view the remaining formulas
use theorem provers to prove the resulting formulas
- some of the provers: cvcl (make symbolic link to cvc3), z3, SPASS, E, Vampire, BAPA, Isabelle (see also –help)

In general, system also deals with:

specification variables (shorthands and ghost variables)
loop invariant inference