Minimization of Deterministic Finite State Machines
We consider deterministic finite state machine 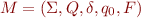 .
.
Goal: build a state machine 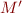 with the least number of states that accepts the language
with the least number of states that accepts the language 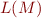 .
.
- we obtain a space-efficient, executable representation of a regular language
This is the process of minimization of  .
.
- an easy case of minimizing size of 'generated code' in compiler
We say that state machine  distinguishes strings
distinguishes strings  and
and  iff it is not the case that (
iff it is not the case that (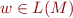 iff
iff 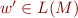 ).
).
Minimization Algorithm
Step 1: Remove unreachable states
We first discard states that are not reachable from the initial state–such states are useless. In resulting machine, for each state  there exists a string
there exists a string  such that
such that  , let
, let  one such string of minimal length.
one such string of minimal length.
(Main) Step 2: Compute Non-Equivalent States
We wish to merge states  and
and  into same group as long as they “behave the same” on all future strings
into same group as long as they “behave the same” on all future strings  , i.e.
, i.e.
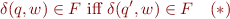
for all  .
.
If the condition  above holds, we called states equivalent. If the condition does not hold, we call states
above holds, we called states equivalent. If the condition does not hold, we call states  ,
, non-equivalent.
non-equivalent.
States  and
and  are
are  -non-equivalent if it is not the case that (
-non-equivalent if it is not the case that ( ).
).
Two states are non-equivalent iff they are  -non-equivalent for some string
-non-equivalent for some string  .
.
Observe that
- if
 and
and 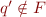 then
then  and
and  are
are  -non-equivalent
-non-equivalent - if
 and
and  are
are  -non-equivalent and we have
-non-equivalent and we have 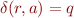 ,
, 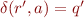 for some symbol
for some symbol  , then
, then  and
and  are
are  -non-equivalent
-non-equivalent - conversely, if
 and
and  are
are  -non-equivalent and
-non-equivalent and  is not an empty string, then for
is not an empty string, then for  the states
the states 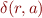 and
and 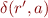 are
are  -non-equivalent
-non-equivalent
These observations lead to an iterative algorithm for computing non-equivalence relation 
- initially put
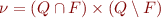 (only final and non-final states are initially non-equivalent)
(only final and non-final states are initially non-equivalent) - repeat until no more changes: if
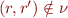 and there is
and there is  such that
such that 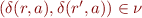 , then
, then
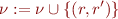
Step 3: Merge States that are not non-equivalent
Relation 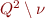 is an equivalence relation
is an equivalence relation  . We define the 'factor automaton' by merging equivalent states:
. We define the 'factor automaton' by merging equivalent states:
- the initial state is
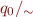
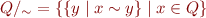
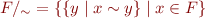
- relation
![Math $r = \{ ([x],[y]) \mid (x,y) \in \delta \}$](/w/lib/exe/fetch.php?media=wiki:latex:/img91457ee4e7ecc7773230679b756150fb.png) is a function, and we can use it to define a new deterministic automaton (there is a transition in the resulting automaton iff there is a transition between two states in the original automaton)
is a function, and we can use it to define a new deterministic automaton (there is a transition in the resulting automaton iff there is a transition between two states in the original automaton)
This is the minimal automaton.
Correctness of Constructed Automaton
Clearly, this algorithm terminates because in worst case all states become non-equivalent. We will prove below that the resulting value  is the non-equivalence relation, i.e. the complement of relation given by
is the non-equivalence relation, i.e. the complement of relation given by  above.
above.
By induction, we can easily prove that if 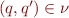 , then
, then  and
and  are non-equivalent. Similarly we can show that if
are non-equivalent. Similarly we can show that if  and
and  are
are  -non-equivalent for
-non-equivalent for  of length
of length  , then
, then 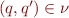 by step
by step  of the algorithm. Because the algorithm terminates, this completes the proof that
of the algorithm. Because the algorithm terminates, this completes the proof that  is the non-equivalence relation.
is the non-equivalence relation.
Consequently, 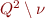 is the equivalence relation. From the definition of this equivalence it follows that if two states are equivalent, then so is the result of applying
is the equivalence relation. From the definition of this equivalence it follows that if two states are equivalent, then so is the result of applying  to them. Therefore, we have obtained a well-defined deterministic automaton.
to them. Therefore, we have obtained a well-defined deterministic automaton.
Minimality of Constructed Automaton
Note that if two distinct states are non-equivalent, there is  such that states
such that states 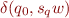 and
and 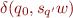 have different acceptance, so
have different acceptance, so  distinguishes
distinguishes 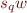 and
and  . Now, if we take any other state machine
. Now, if we take any other state machine 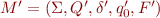 with
with 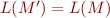 , it means that
, it means that  , otherwise
, otherwise 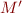 would not distinguish
would not distinguish 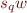 and
and  . So, if there are
. So, if there are  pairwise non-equivalent states in
pairwise non-equivalent states in  , then a minimal finite state machine for
, then a minimal finite state machine for 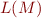 must have at least
must have at least  states. Note that if the algorithm constructs a state machine with
states. Note that if the algorithm constructs a state machine with  states, it means that
states, it means that 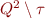 had
had  equivalence relations, which means that there exist
equivalence relations, which means that there exist  non-equivalent states. Therefore, any other deterministic machine will have at least
non-equivalent states. Therefore, any other deterministic machine will have at least  states, proving that the constructed machine is minimal.
states, proving that the constructed machine is minimal.
Example
Construct automaton recognizing
- language {=,<=}
- language {=,<=,==}
Minimize the automaton.