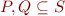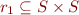Formulas for Representing Sets and Relations
Let the state of programs be 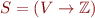 where
where 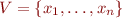 .
.
In Hoare Logic Basics we defined meaning of Hoare triple 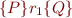 when
when
We also defined the meaning of wp and sp. We next look at these notions when
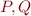 are formulas defining the set of states
are formulas defining the set of states- command
 instead of relation
instead of relation  is used to specify the program
is used to specify the program
Example: Precondition 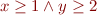 , command
, command 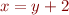 , postcondition
, postcondition  . Initial state has values of x,y equal to
. Initial state has values of x,y equal to 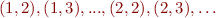 . Relation transforms e.g.
. Relation transforms e.g. 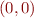 into
into 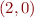 etc. Previously we worked on such sets and relations. Today we work on actual formulas i.e. their syntax trees.
etc. Previously we worked on such sets and relations. Today we work on actual formulas i.e. their syntax trees.
Let  and
and  be formulas in our language
be formulas in our language  and
and  a command, following the syntax of our simple programming language.
a command, following the syntax of our simple programming language.
We define Hoare triples on these syntactic entities by taking their interpretation as sets and relations. Specifically, given definitions in the Hoare Logic Basics, we define
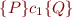
to mean
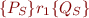
where
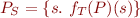 = (informally) =
= (informally) = 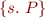
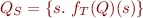 = (informally) =
= (informally) = 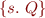
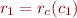 is the meaning of relation given by Relational Semantics
is the meaning of relation given by Relational Semantics
Above, 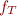 assigns a predicate to the formula according to Relational Semantics and is similar to function
assigns a predicate to the formula according to Relational Semantics and is similar to function 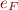 for evaluating formulas in First-order logic semantics.
for evaluating formulas in First-order logic semantics.
Taking into account the definition of Hoare triple for sets 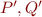 and relation
and relation  , we conclude that
, we conclude that 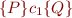 is equivalent to
is equivalent to
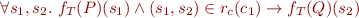
We similarly extend the notion of  and
and 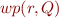 to work on formulas and commands.
to work on formulas and commands.
We use the same notation and infer from the context whether we are dealing with sets and relations or formulas and commands.
To express condition  , we will compute formulas that define relations, following the definition of
, we will compute formulas that define relations, following the definition of  from Relational Semantics.
from Relational Semantics.
Formulas That Specify Relations
To specify relation 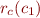 we compute by formula
we compute by formula  containing
containing 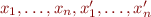 specifying the semantics of c_1, that is, formula
specifying the semantics of c_1, that is, formula  such that, informally,
such that, informally,
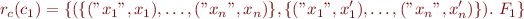
Note that above
 denotes the initial state
denotes the initial state denotes the final state of the command.
denotes the final state of the command.
Denote the truth value of formula in two states by 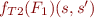 :
:
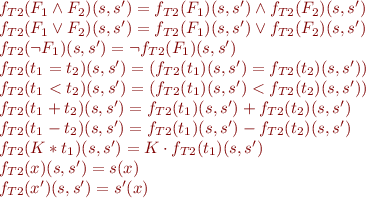
We can then write more precisely the condition for formula 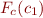 . It should be formula
. It should be formula  such that:
such that:
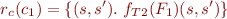
We thus have
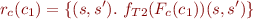
With such notion of 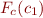 , we represent the validity of a Hoare triple with
, we represent the validity of a Hoare triple with
- precondition

- command

- postcondition

as the validity of the formula:
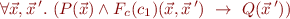
where
 denotes
denotes 
 denotes
denotes 
We next give rules for computing 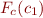 for each (loop-free) command
for each (loop-free) command  .
.