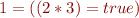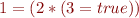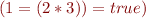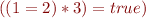Problem 1

Transform the following grammar to Chomsky Normal Form:

$S\rightarrow(S)|A$
$A\rightarrow SS|\epsilon$

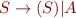
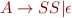
Please give the detailed steps of the algorithm.

Solution

Elimination of non-productive non-terminals:

There are none.

Elimination of unreachable non-terminals:

There are none.

Making non-terminals non-nullable:

$nullable={S,A}$
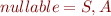
We create production: $S\rightarrow()$ and $A\rightarrow \epsilon$
We eliminate all $\epsilon$ on the right side of rules, removing $A\rightarrow \epsilon$
Because S is nullable, we introduce a new initial symbol S' and add rule $S'\rightarrow S|\epsilon$
We obtain the following new grammar:

$S'\rightarrow S|\epsilon$
$S\rightarrow ()|(S)|A$
$A\rightarrow SS$

Eliminating single productions:

$S'\rightarrow ()|(S)|SS|\epsilon$
$S\rightarrow ()|(S)|SS$

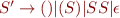
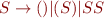
Making non-terminals alone on the right hand side:

$P_{1}\rightarrow($
$P_{2}\rightarrow)$
$S'\rightarrow P_{1}P_{2}|P_{1}SP_{2}|SS|\epsilon$
$S\rightarrow P_{1}P_{2}|P_{1}SP_{2}|SS$

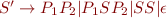
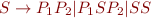
Eliminating non-binary productions:

$P_{1}\rightarrow($
$P_{2}\rightarrow)$
$Q\rightarrow P_{1}S$
$S'\rightarrow P_{1}P_{2}|QP_{2}|SS|\epsilon$
$S\rightarrow P_{1}P_{2}|QP_{2}|SS$

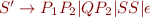
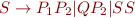
Problem 2

Consider the following grammar:

E ::= E+E
E ::= E*E
E ::= E=E
E ::= Num | true | false

Where Num represents integers.

Run Earley's parsing algorithm on the following input: 1=2*3=true

How many parse trees do you obtain?

Write down those parse trees that are correct according to the following types:

+ : Int x Int→Int

* : Int x Int→Int

= : Bool x Bool → Bool

= : Int x Int → Bool

Solution

$S(0)=\{(S\rightarrow.E\,eof,0),(E\rightarrow.E+E,0),(E\rightarrow.E*E,0),(E\rightarrow.E=E,0),$
$(E\rightarrow Num|true|false,0)\}$

$S(1)=\{(E\rightarrow Num.,0),(S\rightarrowE\,.eof,0),(S\rightarrow E.,0),(E\rightarrow E.+E,0),(E\rightarrow E.*E,0),$
$(E\rightarrow E.=E,0)\}$

$S(2)=\{(E\rightarrow E=.E,0),(E\rightarrow.E+E,2),(E\rightarrow.E*E,2),(E\rightarrow.E=E,2),$
$(E\rightarrow.Num|true|false,2)\}$

$S(3)=\{(E\rightarrow Num.,2),(E\rightarrow E=E.,0),(E\rightarrow E.+E,2),(E\rightarrow E.*E,2),$
$(E\rightarrow E.=E,2),(E\rightarrow E.+E,0),(E\rightarrow E.*E,0),(S\rightarrow.E\,eof,0),(E\rightarrow E.=E,0)\}$

$S(4)=\{(E\rightarrow E*.E,2),(E\rightarrow.E+E,4),(E\rightarrow.E*E,4),(E\rightarrow.E=E,4),$
$(E\rightarrow.Num|true|false,4),(E\rightarrow E*.E,0))\}$

$S(5)=\{(E\rightarrow Num.,4),(E\rightarrow E*E.,2),(E\rightarrow E.+E,4),(E\rightarrow E.*E,4),$
$(E\rightarrow E.=E,4),(E\rightarrow E=E.,0),(E\rightarrow E.+E,2),(E\rightarrow E.*E,2),$
$(E\rightarrow E.=E,2),(E\rightarrow E.+E,0),(E\rightarrow E.*E,0),(E\rightarrow E.=E,0),$
$(E\rightarrow E*E.,0),(E\rightarrow E\, .eof)\}$

$S(6)=\{(E\rightarrow E=.E,4),(E\rightarrow E=.E,2),(E\rightarrow.E+E,6),(E\rightarrow.E*E,6),$
$(E\rightarrow.E=E,6),(E\rightarrow.Num|true|false,6),(E\rightarrow E=.E,0)\}$

$S(7)=\{(E\rightarrow true.,6),(E\rightarrow E=E.,4),(E\rightarrow E=E.,2),(E\rightarrow E.+E,6),$
$(E\rightarrow E.*E,6),(E\rightarrow E.=E,6),(E\rightarrow E*E.,2),(E\rightarrow E.+E,4),$
$(E\rightarrow E.*E,4),(E\rightarrow E.=E,4),(E\rightarrow E=E.,0),(E\rightarrow E.+E,2),$
$(E\rightarrow E.*E,2),(E\rightarrow E.=E,2),(S\rightarrow E\,.eof,0),(E\rightarrow E.+E,0),$
$(E\rightarrow E.*E,0),(E\rightarrow E.=E,0),(E\rightarrow E*E.,0)\}$

$S(8)=\{(S\rightarrow E\, eof.,0)\}$

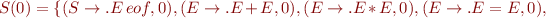
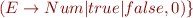
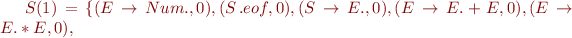
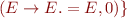
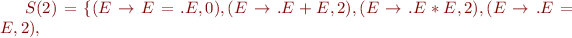
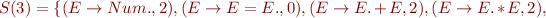
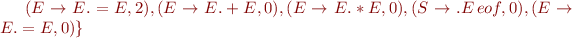
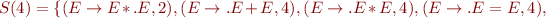
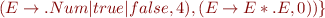
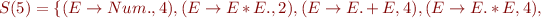
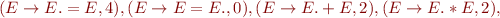
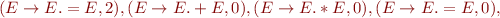
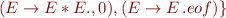
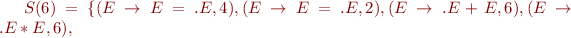
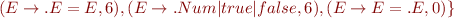
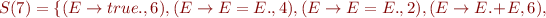
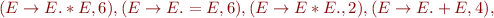
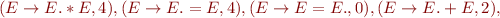
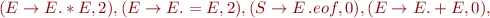
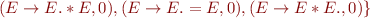
We got 5 parse trees:

$1 = ((2 * 3) = true)$
$1 = (2 * (3 = true))$
$(1 = (2 * 3)) = true)$
$((1 = 2) * 3) = true)$
$(1 = 2) * (3 = true)$

According to types, only one is valid:

$(1 = (2 * 3)) = true)$