LARA

Homework 03

Due Monday, 24th October, 10:15am. Please hand in before the lecture.

Problem 1

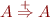A grammar has a cycle if there is a non-terminal $A$ such that $A\stackrel{+}{\Rightarrow}A$, i.e. it is possible to derive the nonterminal A from A by a sequence of production rules.

  • Show that an LL(1) grammar must have no cycles. Recall, that an LL(1) grammar is one for which a predictive parser needs just one look-ahead symbol.
  • Give an algorithm that eliminates cycles in a context-free grammar.

Problem 2

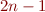Show that if a grammar is in Chomsky normal form then the parse tree for a word of length $n > 0$ has exactly $2n - 1$ interior nodes.

Problem 3

Assume a grammar in Chomsky normal has $n$ non-terminals. Show that if the grammar can generate a word with a derivation having at least $2^n$ steps, then the recognized language should be infinite.

Problem 4

Assume that we want to use the CYK algorithm for the grammars which are not in Chomsky normal form. For example, consider the following grammar for balanced parenthesis: 

S -> ( S )
S -> SS
S -> ()

The diagram below shows the parsing for "(()())" using CYK.

What is the complexity of the CYK algorithm in this case? Describe why it is not a good idea to use CYK for arbitrary grammars not in the Chomsky normal form.

Problem 5

Let {a, b} be terminals, and {A, B} non-terminals. A production is called linear if it is of the form A → aBb. In other words, if the right hand side can contain only one non-terminal. Show that there are context free languages for which no linear grammar exists.