Homework 6
Due Monday, November 21st, 10:10am.
A unit expression is defined by following grammar
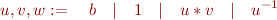
where 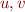 are unit expressions themselves and
are unit expressions themselves and  is a base unit:
is a base unit:

You may use  to denote the set of the unit types
to denote the set of the unit types
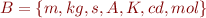
For readability, we use the syntactic sugar
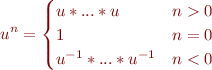
and
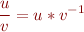
Problem a)
Give the type rules for the arithmetic operations  .
Assume that the trigonometric functions take as argument radians, which are dimensionless (since they are defined as the ratio of arc length to radius).
.
Assume that the trigonometric functions take as argument radians, which are dimensionless (since they are defined as the ratio of arc length to radius).
Problem b)
The unit expressions as defined above are strings, so that e.g.
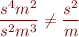
however physically these units match. Define a procedure such that your type rules type check expressions, whenever they are correct according to physics.
Problem c)
Determine the type of  in the following code fragment. The values in angle brackets give the unit type expressions of the variables and
in the following code fragment. The values in angle brackets give the unit type expressions of the variables and 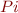 is the usual constant
is the usual constant  in the Scala math library. Give the full type derivation tree using your rules from a) and b), i.e. the tree that infers the types of the variables
in the Scala math library. Give the full type derivation tree using your rules from a) and b), i.e. the tree that infers the types of the variables  .
.
val x: <m> = 800 val y: <m> = 6378 val g: <m/(s*s)> = 9.8 val R = x + y val w = sqrt(g/R) val T = (2 * Pi) / w
Problem d)
Consider the following function that computes the Coulomb force, and suppose for now that the compiler can parse the type expressions:
def coulomb(<(N*m)/(C*C)> k, <C> q1, <C> q2, <m> r): <N> {
return (k* q1 * q2)/(r*r)
}
The derived types are  and
and 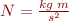 .
Does the code type check? Justify your answer.
.
Does the code type check? Justify your answer.
Problem e)
Suppose you want to use the unit feet in addition to the Si units above. How can you extend your type system to accommodate for this? Explain your answer.
(Assume that 1m = 3.28084 feet.)
Problem f)
For this problem we consider expressions whose free variables have only basic types, i.e. 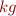 ,
,  , but no compund types like
, but no compund types like  . Assume also that the only operators within expressions are
. Assume also that the only operators within expressions are 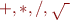 , but that they can be combined in arbitrary ways and be arbitrarily large, as long as they type check.
, but that they can be combined in arbitrary ways and be arbitrarily large, as long as they type check.
Consider such an expression that computes a value of some type  , where
, where  may be compound. Prove the following theorem for this case.
may be compound. Prove the following theorem for this case.
Theorem: Suppose that the result type  does not contain a base unit
does not contain a base unit 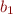 (or, equivalently, this base type occurs only with the overal exponent 0, as
(or, equivalently, this base type occurs only with the overal exponent 0, as  ). If we multiply all variables of type
). If we multiply all variables of type 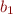 by a fixed numerical constant
by a fixed numerical constant  , the final result of the expression does not change.
, the final result of the expression does not change.
For example, suppose that we want to compute the center of mass  of two objects in 2D, using the following expression:
of two objects in 2D, using the following expression:

Here 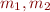 are the masses of the objects in
are the masses of the objects in 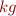 , and
, and 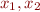 are their distances in
are their distances in  (meters) from some reference point. Because the final result has type
(meters) from some reference point. Because the final result has type  , by the above theorem, we can multiply
, by the above theorem, we can multiply  and
and 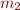 by, e.g.,
by, e.g.,  ; the value
; the value
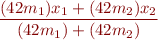
is the same as the previous value. As another example, suppose we estimate a gravity  on Moon by measuring a free fall from height
on Moon by measuring a free fall from height  , then compute the time needed for a free fall from another height
, then compute the time needed for a free fall from another height  , computing
, computing  as
as
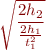
The result type of this expression is  (seconds). Therefore, if we multiply both
(seconds). Therefore, if we multiply both  and
and  by a constant, say 100, the value of this expression does not change.
by a constant, say 100, the value of this expression does not change.
Let us re-state the theorem by introducing a little more notation. If  is an expression (which may contain variables
is an expression (which may contain variables 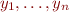 and possibly some other variables), and
and possibly some other variables), and  are expressions, let
are expressions, let

denote the result of replacing in  in
in 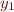 with expression
with expression  , and so on, with
, and so on, with 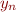 replaced by
replaced by  . The theorem above then says that, under the stated assumptions, for every constant
. The theorem above then says that, under the stated assumptions, for every constant  and all variables
and all variables 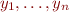 whose type exponent
whose type exponent 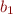 in
in  is zero, the following equality holds for all values of all variables (including
is zero, the following equality holds for all values of all variables (including 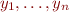 but also variables other than
but also variables other than 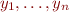 ):
):
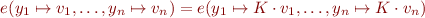
Prove the above theorem.
Note: We assume that neither 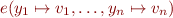 nor
nor
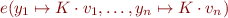 divide by zero or take square roots of negative numbers. You do not need to worry about such errors in this problem.
divide by zero or take square roots of negative numbers. You do not need to worry about such errors in this problem.
Hint: You may need to prove a more general theorem and derive the desired theorem as a consequence.