Homework 02
Due Monday, 17th October, 10:15am. Please hand in before the lecture.
For this homework, recall that a parse tree is a tree that represents the structure of the string to be parsed according to some grammar.
It can be defined recursively as follows:
- If t is a terminal, then t() is a parse tree.
- Given the parse trees t1(…), t2(..), …, t3(…) and a production rule
Y → t1 t2 … t3, then Y(t1(…), t2(…), …, t3(…)) is also a parse tree.
Problem 1
Show that the regular languages can be recognized with LL(1) parsers. Describe a process that, given a regular expression, constructs an LL(1) parser for it.
Problem 2
A grammar is right regular if and only if the production rules are of the following form:
X -> a X -> aY X -> ε
where a is a terminal, X, Y are non-terminals. A left-regular grammar is defined analogously, with the second rule being X → Za.
Consider the following right regular grammar over 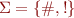 :
:
S -> #A | !# | ! A -> ! | #B | ε B -> #B | !
a) Determine how the input string '###!' is derived.
b) Find a regular expression that accepts the same language as this grammar.
c) Show that a language is regular if and only if there exists a regular grammar that generates it. I.e. show that for each regular expression there is a regular grammar that defines the same language, and vice versa. (A regular grammar is a grammar that is either right or left regular.)
Problem 3
The following grammar is motivated by type definitions in Scala.
TypeDefinition := "type" Identifier "=" Type Type := Type "," Type Type := Type "=>" Type Type := "Int" | "Boolean"
a) By giving at least one input which has two different parse trees prove that the grammar is ambiguous.
b) Given the fact that “=>” has a lower precedence than “,” resolve the ambiguity of the grammar. That is, write a new grammar that determines the same language but is not ambiguous, such that the Type “Int ⇒ Int, Int” is parsed as function from Int to Int,Int.
Problem 4
The following grammar generates all the regular expressions over 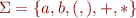 .
.
S -> S S
S -> S '+' S
S -> S '*'
S -> '(' S ')'
S -> 'a' | 'b'
a) Compute the First and Follow sets for S.
b) By giving two different parse trees for an input, show that the grammar is ambiguous.
c) Assuming that the '*' has the highest and '+' has the lowest precedence, find a grammar that accepts the same language but is unambiguous.
d) Compute the First and Follow sets for the non-terminals of the new grammar.
e) Is the new grammar LL(1)?
Problem 5
A grammar is called LL(k) if it needs k tokens of lookahead when parsing a sentence. Does the following grammar belong to LL(k)? Justify your answer and find the smallest k you can, if applicable.
S -> AB S -> BC A -> a A -> Ba B -> Cc C -> c B -> a