Homework 1
Due Wednesday, 5th October, 10:15am. Please hand in to Eva or Giuliano before the labs.
Problem 1
Find a regular expression that generates all alternating sequences of 0 and 1 with arbitrary length (including lengths zero, one, two, …). For example, the alternating sequences of length one are 0 and 1, length two are 01 and 10, length three are 010 and 101. Note that no two adjacent character can be the same in an alternating sequence.
Problem 2
Construct a DFA for the language of well-nested parenthesis with a maximal nesting depth of 3. For example, ε, ()(), (()(())) and (()())()(), but not (((()))) nor (()(()(()))), nor ())) .
By well-nested parentheses we mean those that are correctly nested, and are thus given by the grammar such as the one seen in the class:

Problem 3
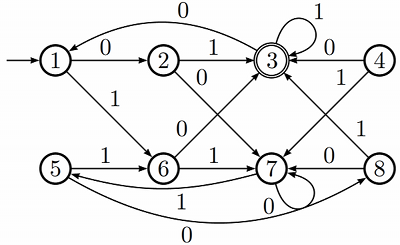
Find two equivalent states in the automaton, and merge them to produce a smaller automaton
that recognizes the same language. Repeat until there are no longer equivalent states.
Recall that the general algorithm for minimizing finite automata works in reverse. First, find all pairs of inequivalent states. States X, Y are inequivalent if X is final and Y is not,
or (by iteration) if  and
and  and X' and Y' are inequivalent. After this iteration ceases to find new pairs of inequivalent states, then X, Y are equivalent, if they are not inequivalent.
and X' and Y' are inequivalent. After this iteration ceases to find new pairs of inequivalent states, then X, Y are equivalent, if they are not inequivalent.
Problem 4
Let  be any deterministic finite automaton. Assume that
be any deterministic finite automaton. Assume that  contains exactly
contains exactly  states. Show that if it accepts at least one string of length
states. Show that if it accepts at least one string of length  or greater then the accepted language is infinite.
or greater then the accepted language is infinite.
Problem 5
Let rtail be a function that returns all the symbols of a string except the last one. For example, rtail(Lexer) = Lexe.
rtail is undefined for an empty string.
If  is a regular expression, then
is a regular expression, then 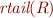 applies the function to all the elements.
For example,
applies the function to all the elements.
For example, 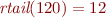 .
.
Prove that 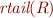 is regular if
is regular if  is not nullable.
is not nullable.
Bonus part: Let  denote the length of the string
denote the length of the string  . Let
. Let  be a regular language. Is the language
be a regular language. Is the language  always regular?
always regular?