Range Analysis Example
Analysis Domain
Continue the example from Sets of States at Each Program Point but instead of allowing to denote all possible sets, we will allow sets represented by expressions
![Equation \begin{equation*}
[L, U]
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imgc6238cca3b0575d272fc4df2548603bf.png)
which denote the set 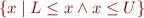 .
.
Thus,  is the lower bound and
is the lower bound and  is the upper bound. To ensure that we have only a few elements, we let
is the upper bound. To ensure that we have only a few elements, we let
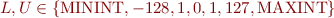
Example: ![Math $[0,127]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgc2976702eeddf84e7113a8e500e35403.png) denotes integers between
denotes integers between  and
and 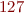 .
.
Furthermore, ![Math $[\mbox{MININT},\mbox{MAXINT}]$](/w/lib/exe/fetch.php?media=wiki:latex:/img21cb0da5bf34d6bf36840e01af2ccf77.png) denotes all possible integers, and we denote it
denotes all possible integers, and we denote it  .
.
Instead of writing ![Math $[1,0]$](/w/lib/exe/fetch.php?media=wiki:latex:/img767690ac8ef373e6ec06ef8b7e47ee21.png) and other empty sets, we will always write
and other empty sets, we will always write  , whose meaning is empty set, and therefore require that in
, whose meaning is empty set, and therefore require that in ![Math $[L,U]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgd71369fd4630ca9ce95b2c4db8960a33.png) we have that
we have that 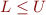 .
.
So, we only work with a finite number of sets
Denote the family of these sets by  (domain).
(domain).
Initial Sets
Updating Sets
Now we want to write the same set of equations. But because we have only a finite number of sets, we must approximate. We approximate sets with possibly larger sets.
 denotes the approximation of
denotes the approximation of  : it is the set that contains both
: it is the set that contains both  and
and  , that belongs to
, that belongs to  , and is otherwise as small as possible.
, and is otherwise as small as possible.
Also, we need to use approximate functions 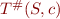 that give result in
that give result in  .
.
Now we replace the equations in Sets of States at Each Program Point with approximate equations:
![Equation \begin{equation*}
\begin{array}{l}
S^\#(a) = \top \\
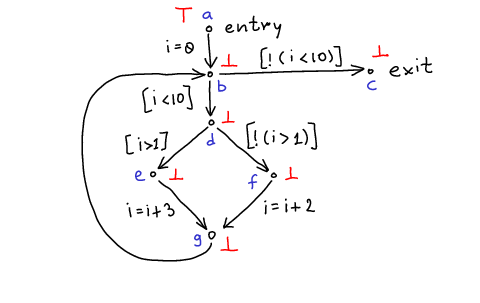
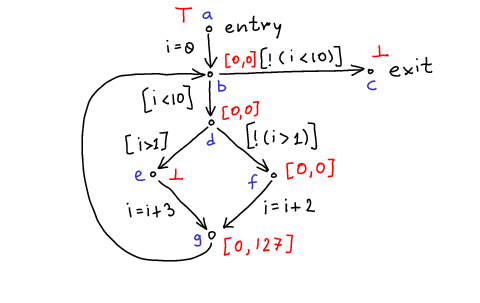
S^\#(b) = T^\#(S^\#(a),i=0) \sqcup T(S(g),skip) \\
S^\#(c) = T^\#(S^\#(b),[\lnot(i<10)]) \\
S^\#(d) = T^\#(S^\#(b),[i<10]) \\
S^\#(e) = T^\#(S^\#(d),[i>1]) \\
S^\#(f) = T^\#(S^\#(d),[\lnot(i>1)]) \\
S^\#(g) = T^\#(S^\#(e),i=i+3) \sqcup T(S(f),i=i+2)
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imge8eddc675d011910fa63011ed5afb036.png)
We solve the equations by starting in the initial state and repeatedly applying them. One can prove that (because this computation is monotonic), the sequence is growing and must terminate (in worst case when all sets are  ).
).
Sets after first iteration:
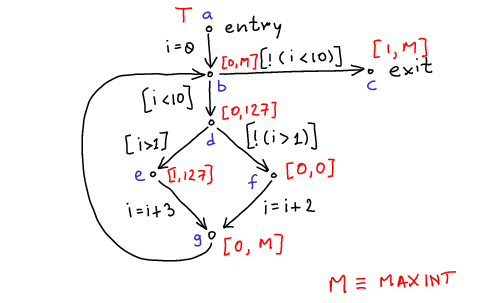
Final values of sets:
Note:
- analysis terminates even if the original program does not terminate or takes very long (important for a compiler!)
- it proves that:
- in all executions i=0 at point

 cannot be zero at point
cannot be zero at point 
- value of
 is always non-negative
is always non-negative
With a larger domain  we can get better results, but analysis can take longer.
we can get better results, but analysis can take longer.