Translate the following function to JVM instructions.

def middle(small: Int, big: Int): Int = {
  val mid = small + (big - small) / 2
  return mid	
}

• Translate the for-loop and if-condition to branch instructions. You can keep all the other statements in . You can also assume that the for loop is translated into the corresponding while loop.
• Now convert the following code fragments to byte code:
  • loop stopping condition from line 3
  • if-statement condition on line 4
  • line 7

 1: def bubblesort( xs : Array[Int]) : Array[Int] = {
 2:  for( i <- 0 until (xs.length - 1))
 3:    for( j <- 0 until (xs.length - i - 1))
 4:      if( xs(j) > xs(j+1)) {
 5:        var tmp = xs(j)
 6:        xs(j) = xs(j + 1)
 7:        xs(j + 1) = tmp
 8:      }
 9:  xs
10:}

The JVM instructions for getting the length of the array in the local slot x are

1: aload_x
2: arraylength

and the instruction to access the ith element of the array xs, i.e. xs(i) is

1: aload_x
2: iload_y
3: iaload

where x is the slot of the array and y the slot of the index i.

Draw the control-flow graph for the following program.

x := 0;
while (x < 10) {
  x := x + 3;
}
if (x >= 0) {
  if (x <= 15) {
    a[x]=7; // made sure index is within range
  } else {
    // v1
    error;
  }
} else {
  // v2
  error;
}

Run range analysis that maintains an interval for at each program point in the control flow graph. Assume that the ranges that the integers can take are [-128, 127] for simplicity, i.e. all intervals within this range are allow, for instance [-1, 3].

What are the fixpoint values at program points marked and ?

Live-Variable Analysis

The GCD of two numbers can be computed using the Euclid algorithm.

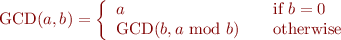
We can implement the GCD algorithm with temporary variables as the following.

x1 := a
x2 := b
Start: if x2 = 0 jump Done
x3 := x1 % x2
x1 := x2
x2 := x3
jump Start
Done: return x1

• Construct the control-flow graph
• Determine the set of live variables before and after the execution of each instruction.