Notion of Subtyping
Subtypes as Subsets
In systems we have formally studied so far, each expression had exactly one type, such as 'int' or 'int → bool'
- this is not case any more in systems with subtyping
We can often think of a type  as approximating the set of values
as approximating the set of values 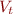 to which an expression can evaluate
to which an expression can evaluate
- statement
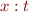 corresponds to
corresponds to 
What are the sets 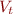 like?
like?
- in previous systems, distinct types denoted disjoint sets: if
 then
then 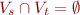
- in more complex systems, these sets overlap
We write  , saying s is a subtype of t to correspond to
, saying s is a subtype of t to correspond to 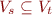
For function types, we assume that functions are defined on all arguments and that 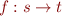 means
means

There are type systems that have intersections and unions, roughly corresponding to  and
and 
Subtyping as a Syntactic Notion
We treat  as a (potentially arbitrary) relation on the set of types, but we aim to define type system such that the following 'weakening' rule holds:
as a (potentially arbitrary) relation on the set of types, but we aim to define type system such that the following 'weakening' rule holds:
 and
and 
then also 
Two ways to ensure the weakening rule:
First way: introduce explicitly a general subtyping rule
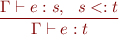
Second way: construct the remaning rules so that the subtyping rule follows as a consequence
In any case, we can use the same general methodology for Proving Safety Properties using Types
- the meaning of type is 'something that makes program type check'
- by soundness, if program type checks, then program has some good properties
Illustrative Example: Positive and Negative Integer Types
Suppose that we have arbitrary-precision integers denoted by 'int'. Then
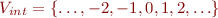
Introduce 'pos' with
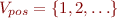
and 'neg' with
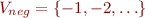
Suppose int,pos,neg are the only types
We have

and

Assuming that 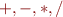 are special constructs (and not just
variables as in lambda calculus), we have the following
rules (fixing some environment
are special constructs (and not just
variables as in lambda calculus), we have the following
rules (fixing some environment  ):
):
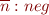 for every
for every 
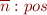 for every
for every 
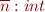 for every
for every 
Let  denote arithmetic expressions.
denote arithmetic expressions.
Some of the rules:
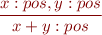
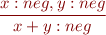
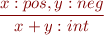
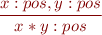
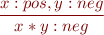
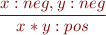
For every type  ,
,
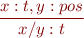
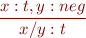
Note that these rules will prevent division by zero
What if we wish to check whether an integer is positive or negative?
- introduce ifpos and ifneg operations:
- (ifpos x y z) evaluates to y if x is positive and to z otherwise
- inside y, we know that x is positive
- here x must be a variable (not a complex expression)
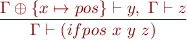
Example: Expression
(ifpos x (y / x) (x + 1))
will never cause division by zero or any other arithmetic error.
Moreover, we can type check e.g. operations on fractions represented as a pair (p,q) of integer p and a positive integer q, with the meaning p/q :
def multiplyFractions(p1 : int, q1 : pos, p2 : int, q2 : pos) : (int,pos) { (p1*q1, q1*q2) } def addFractions(p1 : int, q1 : pos, p2 : int, q2 : pos) : (int,pos) { (p1*q2 + p2*q1, q1*q2) } def printApproxValue(p : int, q : pos) = { print(p/q) // no division by zero }
More sophisticated types can track intervals of numbers and ensure that a program does not crash with an array out of bounds error.