Exercises 1
Exercise 1
Assume the following extensions to the regular expressions. In each case describe why the modification does not actually change the expressibility.
- The intersection of two regular expressions.
- The optional expression
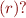 denoting that expression
denoting that expression  optional
optional - Limiting Kleene repetition with a maximum and minimum bound
Design your own operator that extends regular expressions to make it possible to express nested comments.
Exercise 2
Exercise 3
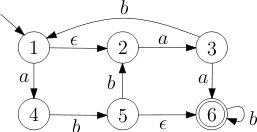
Integer literals are in three forms in Scala: decimal, hexadecimal and octal. The compiler discriminates different classes from their beginning. Decimal integers are started with a non-zero digit. Hexadecimal numbers begin with 0x or 0X and may contain the digits from 0 through 9 as well as upper or lowercase digits A to F afterwards. If the integer number starts with zero, it is in octal representation so it can contain only digits 0 through 7. There can be an l or L at the end of the literal to show the number is Long.
- Draw a single DFA that accepts all the allowable integer literals.
- Write the corresponding regular expression.
Exercise 4
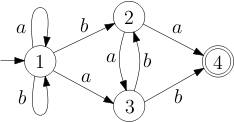
Design a DFA which accepts all the binary numbers divisible by 6. For example your automaton should accept the words 0, 110 (6 decimal) and 10010 (18 decimal).
Exercise 5
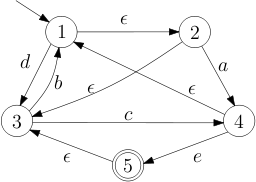
Let  be the language of strings on
be the language of strings on 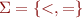 defined by
defined by 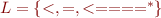 that is,
that is,  .
.
- Construct a DFA that accepts
 .
. - Describe how the lexical analyzer will tokenize the following inputs.
- <=====
- ==<==<==<==<==
- <=====<