Sets of States at Each Program Point
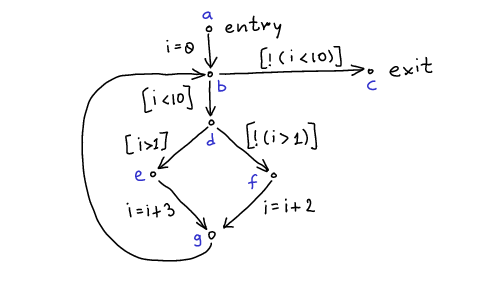
Consider the program
i = 0; while (i < 10) { if (i > 1) i = i + 3; else i = i + 2; }
A possible corresponding control-flow graph is:
Suppose that
- program state is given by the value of the integer variable i
- initially, it is possible that i has any value
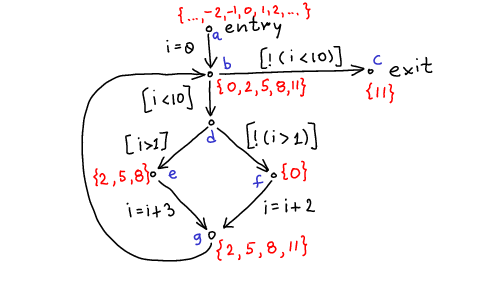
Compute the set of states at each vertex in CFG
For each program point 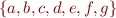 we associate a set of states
we associate a set of states 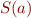 ,
, 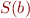 , …,
, …, 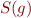 .
.
Running the Program
One way to describe the set of state: for each initial state, run the CFG with this state and insert the modified states at appropriate points.
Reachable States as A Set of Recursive Equations
If  is the label on the edge of the graph, let
is the label on the edge of the graph, let 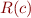 denote the relation between initial and final state that describes the meaning of statement. For example,
denote the relation between initial and final state that describes the meaning of statement. For example,
![Equation \begin{equation*}
\begin{array}{l}
R(i=0) = \{ (i,i') \mid i' = 0 \} \\
R(i=i+2) = \{ (i,i') \mid i' = i+2 \} \\
R(i=i+3) = \{ (i,i') \mid i' = i+3 \} \\
R([i<10]) = \{ (i,i') \mid i'=i \land i < 10 \} \\
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img89dc9aad472446fdf02089fa4ef665b2.png)
We will write 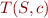 for the image of set
for the image of set  under relation
under relation 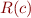 . For example,
. For example,
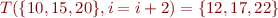
Note that that if [p] is a condition (as generated by 'if' and 'while') then
![Equation \begin{equation*}
T(S, [p]) = \{ x \in S \mid p \}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img65f4efd6457bfb74aa738e9c7aa00361.png)
If an edge has no label, we denote it skip. So, 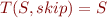 .
.
Now, we can describe the meaning of our program using recursive equations:
![Equation \begin{equation*}
\begin{array}{l}
S(a) = \{ \ldots, -2, -1, 0, 1, 2, \ldots \} \\
S(b) = T(S(a),i=0) \cup T(S(g),skip) \\
S(c) = T(S(b),[\lnot(i<10)]) \\
S(d) = T(S(b),[i<10]) \\
S(e) = T(S(d),[i>1]) \\
S(f) = T(S(d),[\lnot(i>1)]) \\
S(g) = T(S(e),i=i+3) \cup T(S(f),i=i+2)
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img9e8c0557c24eb2b2171703089bc69a53.png)
Note that the solution we computed satisfies the recursive equations. In fact, our solution is the unique least solution of these equations.
The problem with these exact equations is that they are as difficult to compute as running the program on all possible input states. Instead, when we do data-flow analysis, as with type systems, we will consider approximate descriptions of these sets of states.