Widening and Narrowing in Variable Range Analysis
Interval analysis domain, for each program point, maps each program variable to an interval.
Analysis domain has elements  where
where  denotes the set of such intervals.
denotes the set of such intervals.
Height of lattice for unbounded integers: infinite.
Height of lattice of one interval for 64-bit integers: around 
Moreover, if we have  variables in program and
variables in program and  program points, height of lattice for the analysis domain is
program points, height of lattice for the analysis domain is  times larger.
times larger.
How to guarantee (reasonably fast) termination?
Widening technique: if the iteration does not seem to be converging, take a “jump” and make the interval much wider (larger).
Finite set of jump points  (e.g. set of all integer constants in the program)
(e.g. set of all integer constants in the program)
In fixpoint computation, compose  with function
with function
![Equation \begin{equation*}
w([a,b]) = [\max \{x \in J \mid x \le a\},
\min \{x \in J \mid b \le x\}]
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img6af571558de83b412691681a24c9419d.png)
We require the condition:

for all  .
.
The condition holds for the example above.
Approaches:
- always apply widening (we will assume this)
- iterate a few times with
 only (without using
only (without using  ), if we are not at a fixpoint at this program point, then widen.
), if we are not at a fixpoint at this program point, then widen.- this is not monotonic: if you start at fixpoint, it converges, if start below, can jump over fixpoint!
Standard iteration: 
Widening: 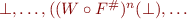
Example where widening works nicely
Consider program:
x = 0; while (x < 1000) { x = x + 1; }
Interval analysis without widening will need around 1000 iterations to converge to interval ![Math $[1000,1000]$](/w/lib/exe/fetch.php?media=wiki:latex:/img1baa212e4e7708e93c889769d4db1bf3.png) for
for  at the end of the program. This
may be too slow.
at the end of the program. This
may be too slow.
Let us derive the set  by taking all constants
that appear in the program, as well as
by taking all constants
that appear in the program, as well as  and
and  :
:
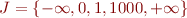
After a few iterations, widening maps interval ![Math $[0,2]$](/w/lib/exe/fetch.php?media=wiki:latex:/img51b74976bf5bf6412f174f5ee6f44494.png) into
into ![Math $[0,1000]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgb979af81a9fe086bfdd9ca6f01d48989.png) . This gives
. This gives ![Math $[0,999]$](/w/lib/exe/fetch.php?media=wiki:latex:/imga8671622a3f4d18956abc8edf62cb7af.png) for
for  at loop entry and again
at loop entry and again ![Math $[1000,1000]$](/w/lib/exe/fetch.php?media=wiki:latex:/img1baa212e4e7708e93c889769d4db1bf3.png) for
for  at
the end of the program, but in many fewer iterations.
at
the end of the program, but in many fewer iterations.
Example showing problems with widening
Consider program:
x = 0; y = 1; while (x < 1000) { x = x + 1; y = 2*x; y = y + 1; print(y); }
Interval analysis without widening will need around 1000 iterations to converge to
![Equation \begin{equation*}
x \mapsto [1000,1000]; \ \ \ \
y \mapsto [1,2001]
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img404134415a3e0e62e29f0eb416f2daaf.png)
This may be too slow.
Now apply widening with the same  as before.
When within loop we obtain
as before.
When within loop we obtain ![Math $x \mapsto [0,1000]$](/w/lib/exe/fetch.php?media=wiki:latex:/img393c479ef48c6ebce0843990a055a624.png) , applying widening function to the interval
, applying widening function to the interval ![Math $[0,2000]$](/w/lib/exe/fetch.php?media=wiki:latex:/imge0fdd1a0057cd9173e538c53ca06bc97.png) for
for  results in
results in  .
We obtain
.
We obtain 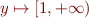 at the end of the program:
at the end of the program:
![Equation \begin{equation*}
x \mapsto [1000,1000]; \ \ \ \
y \mapsto [1,+\infty)
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imged63cffec3ec13db4d55121173660abd.png)
Narrowing
Observation
Consider a monotonic function, such as 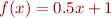 on the set of real numbers. If we consider a sequence
on the set of real numbers. If we consider a sequence 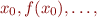 this sequence is monotonically increasing iff
this sequence is monotonically increasing iff  (e.g. for
(e.g. for 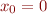 ) and it is monotonically decreasing iff
) and it is monotonically decreasing iff  (e.g. for
(e.g. for 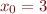 ). Informally, the sequence continues of the direction in which it starts in the first step.
). Informally, the sequence continues of the direction in which it starts in the first step.
This is because  implies by monotonicity of
implies by monotonicity of  that
that  etc., whereas
etc., whereas  implies
implies  .
.
The Idea
Let 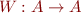 such that
such that  .
.
After finding fixpoint of 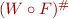 , apply
, apply  to improve precision.
to improve precision.
Widen and Narrow
Lemma: Let  and
and  be monotonic functions on a partial order
be monotonic functions on a partial order  such that
such that  for all
for all  . Define the following:
. Define the following:
where we also assume that the two  and one
and one  exist. Then
exist. Then
 .
.
Proof:
By induction, for each  we have
we have
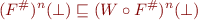
Thus by Comparing Fixpoints of Sequences, we have  .
.
Next, we have that
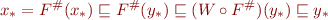
Thus, 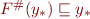 . From there by induction and monotonicity of
. From there by induction and monotonicity of  we obtain
we obtain
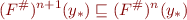
i.e. the sequence 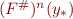 is decreasing. Therefore,
is decreasing. Therefore, 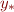 is its upper bound and therefore
is its upper bound and therefore  .
.
On the other hand, we have by monotonicity of  , the fact
that
, the fact
that  is fixpoint, and
is fixpoint, and  that:
that:
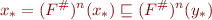
Thus,  is the lower bound on
is the lower bound on 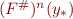 , so
, so  .
.
End of proof.
Note: even if  does not exist, we can simply compute
does not exist, we can simply compute 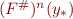 for any chosen value of
for any chosen value of  , it is still a sound over-approximation, because it approximates
, it is still a sound over-approximation, because it approximates  , which approximates the concrete value:
, which approximates the concrete value:

so
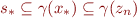
Being able to stop at any point gives us an anytime algorithm.
Example
Example showing how narrowing may improve result after widening
In the above example for the program, the results obtained using widening are:
x = 0; y = 1; // x -> [0,0], y -> [1,1] // (merge point) // x -> [0,1000], y -> [1,+infty) while (x < 1000) { // x -> [0,999], y -> [1,+infty) x = x + 1; // x -> [0,1000], y -> [1,+infty) y = 2*x; // x -> [0,1000], y -> [0,+infty) y = y + 1; // x -> [0,1000], y -> [1,+infty) print(y); } // x -> [1000,1000], y -> [1,+infty)
Let us now apply one ordinary iteration, without widening. We obtain:
x = 0; y = 1; // x -> [0,0], y -> [1,1] // (merge point) // x -> [0,1000], y -> [1,2001] while (x < 1000) { // x -> [0,999], y -> [1,+infty) x = x + 1; // x -> [0,1000], y -> [1,+infty) y = 2*x; // x -> [0,1000], y -> [0,2000] y = y + 1; // x -> [0,1000], y -> [1,2001] print(y); } // x -> [1000,1000], y -> [1,2001]
Thus, we obtained a good first approximation by a few iterations with widening and then improved it with a single iteration without widening.
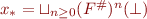
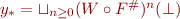

 (by
(by