Reasoning about Procedures by Inlining Contracts
Suppose we have a program where each procedure has a contract. We prove program correctness in two steps:
- replace each procedure call with procedure contract (if there are parameters, instantiate them)
- for each procedure, show that the resulting body satisfies the contract
It is clear that this reasoning is correct for non-recursive procedures.
We will show that it is also correct for mutually recursive procedures.
Example of Inlining Contracts
In this code,
proc even()
requires x >= 0
ensures (wasEven == (old(x) % 2 == 0))
{
if (x==0) {
wasEven = true;
} else {
x = x - 1;
odd();
}
}
proc odd()
requires x >= 0
ensures (wasEven == (old(x) % 2 != 0))
{
if (x==0) {
wasEven = false;
} else {
x = x - 1;
even();
}
}
After inlining contracts we obtain:
proc even()
requires x >= 0
ensures (wasEven == (old(x) % 2 == 0))
{
if (x==0) {
wasEven = true;
} else {
x = x - 1;
x0 = x;
assert(x >= 0);
havoc x, wasEven;
assume(wasEven == (x0 % 2 != 0));
}
}
proc odd()
requires x >= 0
ensures (wasEven == (old(x) % 2 != 0))
{
if (x==0) {
wasEven = false;
} else {
x = x - 1;
x0 = x;
assert(x >= 0);
havoc x, wasEven;
assume(wasEven == (x0 % 2 == 0));
}
}
In the resulting code there are no more procedure calls. We verify for each procedure that it conforms to the pre/post condition. We do so by assuming 'requires' and asserting 'ensures'. We also need to save the initial state to be able to refer to it in the postcondition. For 'even' procedure, we need to show that the following code does not lead to errors:
oldx = x;
assume(x >= 0);
if (x==0) {
wasEven = true;
} else {
x = x - 1;
x0 = x;
assert(x >= 0);
havoc x, wasEven;
assume(wasEven == (x0 % 2 != 0));
}
assert((wasEven == (oldx % 2 == 0));
Correctness of Inlining Contracts
Suppose we have two mutually recursive procedures, as in the previous example. We can give their semantics as the least solution 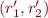 of the system of equations on relations:
of the system of equations on relations:
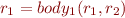
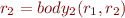
That is, it is the least fixpoint of function
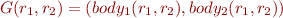
Suppose  has the contract (specification)
has the contract (specification) 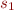 and
and  has contract
has contract  . Inlining contract into first procedure we obtain
. Inlining contract into first procedure we obtain 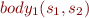 . The technique that we propose therefore corresponds to proving:
. The technique that we propose therefore corresponds to proving:
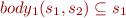
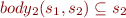
In other words, it shows 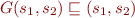 . This means that the specification
. This means that the specification 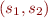 is a postfix point of
is a postfix point of  . By Tarski's Fixpoint Theorem, the least fixpoint is the least postfix point as well, so
. By Tarski's Fixpoint Theorem, the least fixpoint is the least postfix point as well, so
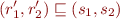
that is  and
and  . Therefore, the meaning of each procedure satisfies its specification, which shows that this approach is correct.
. Therefore, the meaning of each procedure satisfies its specification, which shows that this approach is correct.
Shunting rules
We say that relation  respects errors if for an error state
respects errors if for an error state  we have
we have 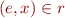 for all states
for all states  .
.
For relations  ,
,  that respect errors, we have
that respect errors, we have


For more, see the semantics of Assert and error conditions.
Proofs:
- using relations
- using weakest preconditions (see homework in SAV'07)
Verifying that Body Conforms to Contract
Consider a program with only one state variable  .
.
We express our approximation as
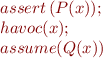
We show that
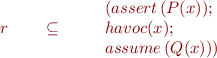
is implied by
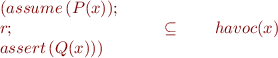
To check the final condition, because  describes the entire state, all we need to check is that the transformed program
describes the entire state, all we need to check is that the transformed program
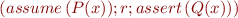
cannot result in assertion violations.
Note: we can also directly check the relation subset condition, by computing formula for relation body and showing that it implies the formula for the contract.