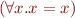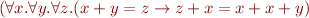Definition of Quantifier Elimination
In this section, we will consider some language  and some set
and some set  of formulas such that
of formulas such that 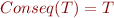 (see First-Order Logic Semantics).
(see First-Order Logic Semantics).
Informal summary: the meaning of relations and functions such as <,+, can be defined by starting from first-order logic, and then introducing a set of axioms in first-order logic that they satisfy, and taking also their consequences. The set of axioms and consequences that define the operations and relations of interest is the theory. Formally, the theory is simply any set of fully quantified formulas (often the theory is understood to also include all of its consequences).
As a special case, we can have
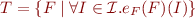
where  is a set of interpretations of interest.
Then
is a set of interpretations of interest.
Then 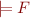 reduces to
reduces to 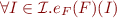 .
If we look at one interpretation, then
.
If we look at one interpretation, then  contains only that interpretation and the condition
contains only that interpretation and the condition 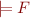 means
means 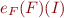 .
.
Shorthand: We will generally fix  and write
and write 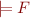 as a shorthand for
as a shorthand for  .
.
Example: Let 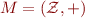 be the structure of integers with addition. If we let
be the structure of integers with addition. If we let 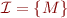 then
then  in the definition above is the set of all formulas involving only
in the definition above is the set of all formulas involving only  that are true about integers. In this example,
that are true about integers. In this example,
 contains e.g. formulas
contains e.g. formulas  does not contain e.g. formula
does not contain e.g. formula 
Definition: We say that  admits quantifier elimination iff for every FOL formula
admits quantifier elimination iff for every FOL formula  in
in  there exists some formula
there exists some formula 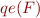 such that
such that

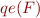 has no quantifiers
has no quantifiers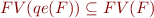
(In words: for every formula there exists an equivalent quantifier-free formula with same free variables.)
Definition: We say that  admits effective quantifier elimination if there is an effectively computable function
admits effective quantifier elimination if there is an effectively computable function  with the property in the previous definition.
with the property in the previous definition.
Definition: A ground formula is a formula  such that
such that
 contains no quantifiers and
contains no quantifiers and 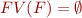 .
.
Example: in language 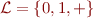 where
where 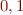 are constants and
are constants and  is a binary operation, an example of a ground formula is
is a binary operation, an example of a ground formula is

Lemma: Suppose that
 has effective quantifier elimination;
has effective quantifier elimination;- there is an algorithm for deciding
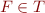 when
when  is a ground formula.
is a ground formula.
Then there is an algorithm for deciding, given a sentence  , whether
, whether 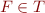 .
.
Proof:
Take  a sentence. Note
a sentence. Note 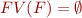 . Compute
. Compute 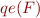 . Note that also
. Note that also  . So
. So 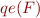 is a ground formula and there is an algorithm to check
is a ground formula and there is an algorithm to check 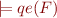 . But
. But 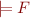 is equivalent to
is equivalent to 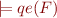 .
.