LARA

Asserts and errors for nice wp definition

We used assert(F) to express conditions that should hold.

Can we give executation semantics to assert?

assert(F) = irrecoverable error if $F$ is false, terminates execution.

wp computes conditions sufficient for errors not to happen.

Postconditions are just asserts at the end of the program.

How to build a system with relations where at the same time 

wp(assert(F),Q) = (F & Q)
wp(assume(F),Q) = (F --> Q)

Then 

wp(assert(false); assume(false),Q) = false
wp(assume(false); assert(false),Q) = true

so cannot have 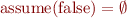$\mbox{assume(false)} = \emptyset$ any more, otherwise both 

assert(false); assume(false)
assume(false); assert(false)

would denote empty relations.

Error Variable and Good States

Introduce variable “error”. Good states are states where this variable has value zero. We write OK for the formula error=0.

We assume that the desired properties $P$ satisfy

\begin{equation*} \models P \rightarrow OK \end{equation*}

Desired Rules for Weakest Preconditions

For all $Q$ such that $\models Q \rightarrow OK$, we would like the following to hold:

\begin{equation*}\begin{array}{l} \models wp(c,Q) \rightarrow OK \\ wp(c1 [] c2,Q) = wp(c1,Q) \land wp(c2,Q) \\ wp(c1 ; c2,Q) = wp(c1,wp(c2,Q)) \\ wp(havoc(x),Q) = \forall x.Q \\ wp(x=e,Q) = Q[x:=e] \\ wp(assume(F),Q) = (OK \land (F \rightarrow Q)) \\ wp(assert(F),Q) = (F \land Q) \end{array}\end{equation*}

We assume above that $x$ is not the error variable.

Note: we wrote $OK \land ...$ in the weakest precondition of assume, but usually $OK$ is implicit and we do not write it. We do not need it in other cases because it follows that right hand side implies $OK$.

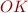Relational Semantics that Fulfills These Rules

Let OK denote s(error)=0 and OK' denote s'(error)=0. We define:

\begin{eqnarray*} R_c(\mbox{havoc(x)}) &=& \{(s,s') \mid OK \rightarrow (OK' \land \bigwedge_{y \not\equiv x}\ s'(y)=s(y)) \} \\ R_c(\mbox{assert}\ F}) &=& \{(s,s') \mid (OK \land F(s)) \rightarrow s=s' \} \\ R_c(\mbox{assume}\ F}) &=& \{(s,s') \mid OK\ \rightarrow\ (F(s) \land s=s') \} \\ R_c(c_1 [] c_2) & = & R_c(c_1) \cup R_c(c_2) \\ R_c(c_1\ ;\ c_2) & = & R_c(c_1) \circ R_c(c_2) \end{eqnarray*}

References