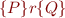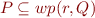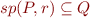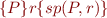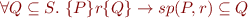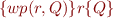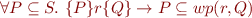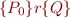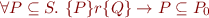Homework 03
Problem 01: Loop unrolling
This programming assignment builds on what you did last time. To help you test your implementation on hand-written programs, we give you a parser and a pretty-printer. Here is the extended AST hierarchy:
/** Terms. The only type in the language is Int. */ sealed abstract class Term case class Constant(c: Int) extends Term case class Variable(v: String) extends Term case class Plus(t1: Term, t2: Term) extends Term case class Minus(t1: Term, t2: Term) extends Term case class Times(c: Int, t: Term) extends Term case class Divide(t: Term, c: Int) extends Term case class Modulo(t: Term, c: Int) extends Term /** Boolean expressions, used as conditions and in assertions/assumptions. */ sealed abstract class BoolExpr case class Equal(t1: Term, t2: Term) extends BoolExpr case class LessThan(t1: Term, t2: Term) extends BoolExpr case class GreaterThan(t1: Term, t2: Term) extends BoolExpr case class Negation(F: BoolExpr) extends BoolExpr case class And(f1: BoolExpr, f2: BoolExpr) extends BoolExpr case class Or(f1: BoolExpr, f2: BoolExpr) extends BoolExpr /** Program commands */ sealed abstract class Command case class Assignment(v: String, t: Term) extends Command case class GetInt(v: String, lb: Int, ub: Int) extends Command case class IfThenElse(cond: BoolExpr, ifcom: Command, elsecom: Command) extends Command case class Block(coms: List[Command]) extends Command case class WhileLoop(cond: BoolExpr, com: Command) extends Command case class Print(str: String, v: String) extends Command case class Skip() extends Command case class Assume(expr: BoolExpr) extends Command case class Assert(expr: BoolExpr) extends Command case class Choice(choice1: Command, choice2: Command) extends Command
Note that:
- We added Assume and Assert statements, the Print statement which was described last time, as well as a Skip statement which can be used, for instance, in empty
elsebranches. - There is a new construct, getInt which we describe below.
- The Block class has changed slightly: it now takes a list of statements. Hopefully your code should be easy to adapt.
- The parser supports Java-like comments,
ifs with noelsebranch, and the operators⇐,>=,!=are desugared into the appropriate trees. - The syntax should be straightforward, but in doubt you can look at the string representation of tokens in
Lexer.scala, or at the demo programs.
As you noticed, there is a new kind of command of the form:
x = getInt(0, 5);
This is a non-deterministic variable assignment: after that command, for every value in the set {0,1,2,3,4,5} there will be an execution where x holds this value in the next step.
Adapt your code
Use this archive, which contains the project structure, a parser and an example program, and adapt your interpreter to it.
You can use ant to compile the code (make sure $SCALA_HOME is set in your environment or edit local.properties), then for instance:
./run.sh demo.while
(un)rollin', rollin', rollin'
Implement an AST transformation which unrolls all loops a certain number of times (see the stub in the archive for the method signature). Use the following idea:
while(cond) { body }
…becomes:
if(cond) { body } if(cond) { body } ... if(cond) { body } assume(!cond);
Problem 02: Non-deterministic Interpreter
Adapt your non-deterministic interpreter to the code we've given you, or if you haven't done it yet, write it according to last week's description (Problem 04).
Your interpreter should now also handle non-deterministic variable assignments using backtracking as for commands. For instance the following program:
// A demo program using all constructs available x = getInt(0, 1); y = getInt(2, 3); z = 0; while (z <= 0) { ( z = 2 * x; [] z = x + y; ) if(z == 1) { z = z - 1; } } println("z is: ", z);
…when unrolled with a factor 2 should result in the following output (again, order doesn't matter):
z is: 2 z is: 2 z is: 2 z is: 3 z is: 3 z is: 4
Some additional remarks:
- Your interpreter can assume the program is loop-free (use loop unrolling first)
- If your interpreter encounters an assumption which does not hold, it should stop silently the current execution, backtrack and go on with the next execution.
- If your interpreter encounters an assertion which does not hold, it should complain about it, backtrack etc.
Problem 03: Proving Properties of sp and wp
For sets  ,
,  , assuming the definition of Hoare triple
, assuming the definition of Hoare triple
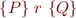
as
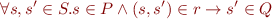
and assuming the definition
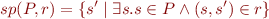
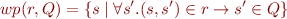
Prove that the following statements from Hoare Logic Basics hold. You can prove statements in any order and use previous results to prove the next ones, as long as you obtain a correct mathematical proof for all the properties.
a)
The following three conditions are equivalent:
b)
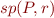 is the strongest among the postconditions of
is the strongest among the postconditions of  with respect to
with respect to  , that is:
, that is:
c)
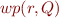 is the weakest among the preconditions of
is the weakest among the preconditions of  with respect to
with respect to  , that is:
, that is:
d)
If 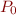 satisfies
satisfies
then 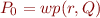 .
.
Problem 04: Counterexamples
Find counterexamples to the following formulas. Feel free to use Alloy, but write down the solution.
a)
For relations  and
and  , find counterexample for:
, find counterexample for:
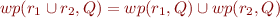
b) - Optional
For 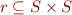 a relation and operators defined as in Sets and Relations, find a counterexample for:
a relation and operators defined as in Sets and Relations, find a counterexample for:
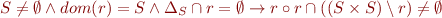
What is the smallest size of the set  for which you can find a counterexample relation
for which you can find a counterexample relation  ?
?