Homework 02
Problem 01: Playing with Alloy
Come up with 2 interesting Alloy formula examples (comparable to examples we have seen in the class):
- one representing valid formula
- one representing invalid formula with a finite counterexample
Explain briefly the results that you obtain when you run the formula in Alloy.
For the valid formula, give a proof why it is valid.
Problem 02: Interpreter
Write an interpreter for our simple programming language extended with assume statement.
The meaning of assignments and control structures is the same as in the usual programming language.
For assume statement, the interpreter should just check whether the condition is true in the current program state. If the condition holds, it should continue. If the condition does not hold, the execution should stop silently.
Use Scala's Int type to represent the unbounded integers in the language.
Your interpreter should take an abstract syntax tree of the program and keep executing the program until it terminates (if it does not terminate, the interpreter should also not terminate). If the program terminates, your interpreter should print the final state of the program.
Here is an example abstract syntax tree that you may wish to use. There is no need to write a parser for this language, you can start from syntax trees. You may modify the syntax tree if needed.
sealed abstract class Term case class Constant(val c: Int) extends Term case class Variable(val v: String) extends Term case class Plus(val t1: Term, val t2: Term) extends Term case class Minus(val t1: Term, val t2: Term) extends Term case class Times(val c: Int, val t: Term) extends Term case class Divide(val t: Term, val c: Int) extends Term case class Modulo(val t: Term, val c: Int) extends Term sealed abstract class BoolExpr case class Equal(val t1: Term, val t2: Term) extends BoolExpr case class LessThan(val t1: Term, val t2: Term) extends BoolExpr case class GreaterThan(val t1: Term, val t2: Term) extends BoolExpr case class Negation(val F: BoolExpr) extends BoolExpr case class And(val f1: BoolExpr, val f2: BoolExpr) extends BoolExpr case class Or(val f1: BoolExpr, val f2: BoolExpr) extends BoolExpr sealed abstract class Command case class Assignment(val v: String, val t: Term) extends Command case class IfThenElse(val cond: BoolExpr, val ifcom: Command, val elsecom: Command) extends Command case class Block(val com1: Command, val com2: Command) extends Command case class WhileLoop( cond: BoolExpr, val com: Command) extends Command
Write syntax tree of a program containing at least two loops and test the execution of your interpreter on this program.
To test the execution, add a 'print' statement that prints a given string and a given integer on the screen.
Problem 03: Computing Relations for Assignments
Using Relational Semantics and the previous syntax tree, write a Scala function that takes
- an assignment statement syntax tree node
- list of all variables that exist in the program
The function should produce a formula describing the relational semantics of the statement.
In the relation, denote the initial value of variable by “old_” prefix, and final value by the variable itself. For example, given statement
x = x + y;
and variables 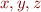 the formula you should obtain should be
the formula you should obtain should be
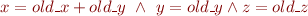
Optional Problem 04: Non-deterministic interpreter (may become mandatory next week)
Add non-deterministic choice [] to syntax tree, in the form of:
case class Choice(choice1: Command, choice2: Command) extends Command
Use backtracking to execute non-deterministic choice: first execute choice1 and continue program execution, then execute choice2 and continue with program execution.
For example, if the interpreter runs on the syntax tree for the following program
x = 0;
(x = x + 10; [] x = x + 40;)
(x = 2 * x; [] x = 10 * x;)
println("x=", x);
the result should be some permutation of the following four lines:
x=20 x=100 x=80 x=400
That is, each of the four lines must appear in the output exactly once, and no other line should appear.
Write a function that takes program tree with IfThenElse nodes and eliminates IfThenElse by replacing them using Choice and Assume, according to Relational Semantics.
Show an example IfThenElse. Then check that your interpreter gives the same result for IfThenElse and its translation.