Bounding Variables in Presburger Arithmetic
We can use insights from quantifier elimination to obtain alternative algorithms for deciding formulas.
Define 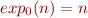 and
and 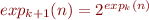 for all
for all 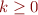 .
.
Bounds Showing Membership in 2EXPSPACE
Let 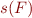 denote the maximum of the constant
denote the maximum of the constant  and of all constants ocurruring in the formula
and of all constants ocurruring in the formula  .
.
Theorem (Oppen): There exists a constant  such that the following is true. If
such that the following is true. If  is a formula of Presburger arithmetic with
is a formula of Presburger arithmetic with  quantifiers,
then when Cooper's procedure is applied to
quantifiers,
then when Cooper's procedure is applied to  , every integer constant encountered is bounded by
, every integer constant encountered is bounded by
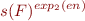
Lemma (Ferrante, Rackhoff): There exists a constant  such that the following is true. Let
such that the following is true. Let  be the formula
be the formula
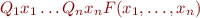 , where
, where  is quantifier-free and
is quantifier-free and  is
is  or
or  for each
for each  ,
, 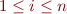 ,
and let
,
and let 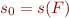 . Then
. Then  is true iff
is true iff
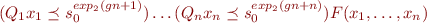
where  means
means  .
.
Bounded Quantifier Alternation
Example: if  has no quantifiers, then these two formulas have one quantifier alternation:
has no quantifiers, then these two formulas have one quantifier alternation:
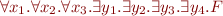

and this formula has two quantifier alternations:
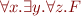
Definition:
A formula in prenex form has  quantifier alternations iff it is the form
quantifier alternations iff it is the form
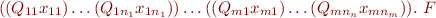
where for the same  , all quantifiers
, all quantifiers 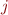
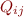 are the same type (either all are
are the same type (either all are  or all are
or all are  ), and for
), and for  and
and  the quantifiers are of different type.
the quantifiers are of different type.
Theorem (Reddy, Loveland, 1978): If  is a closed Presburger arithmetic formula
is a closed Presburger arithmetic formula  of size
of size  with
with  quantifier alternations, where
quantifier alternations, where 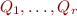 are quantifiers and
are quantifiers and  is quantifier-free, then
is quantifier-free, then  is true iff the formula
is true iff the formula
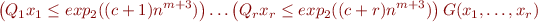
with bounded quantifiers is true for some  .
.
In general, it is often quantifier alternations that cause high complexity of the decision procedure, not quantifiers themselves.
References
- Reddy, Loveland: Presburger Arithmetic with Bounded Quantifier Alternation, pdf
- Lararuk, Sturm: Weak quantifier elimination for the full linear theory of the integers, pdf
- Ferrante, Rackoff: A Decision Procedure for the First-Order Theory of Addition with Order, pdf (NOTE: this is for real numbers, not integers)