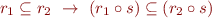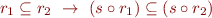This is an old revision of the document!
Relational Semantics of Procedures
Let  be the set of states and
be the set of states and  denote
denote 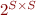 , the set of all relations on
, the set of all relations on  .
.
In Relational Semantics for a language without procedures we had semantic function that maps programs to relations \[
r_c : C \to {\cal R}
\]
so 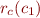 was the relation corresponding to the command
was the relation corresponding to the command  , and we denote it by
, and we denote it by ![Math $[\![c_1]\!]$](/w/lib/exe/fetch.php?media=wiki:latex:/img221f53b47ce4a0fa85fbc98feaac35d1.png) .
.
How can we define semantics for program with recursive procedures?
One Recursive Procedure
We first illustrate the semantics for one recursive procedure. The definition only relies on the Lattices structure, so it generalizes to recursive definitions with multiple procedures, and recursive definitions in general.
Example: Consider the following procedure that, if  are positive, moves the content of x into y.
are positive, moves the content of x into y.
var x,y;
proc move() {
if (x > 0) {
x = x - 1;
move();
y = y + 1;
}
}
or, expressed using non-deterministic choice and assume:
var x,y;
proc move() {
( assume(x>0);
x = x - 1;
move();
y = y + 1;
)
[] (assume (!(x>0))
}
Suppose we have relation  describing the meaning of the procedure. By Relational Semantics, this procedure should behave similarly as the meanings of commands, so we should have the following equation:
\[
describing the meaning of the procedure. By Relational Semantics, this procedure should behave similarly as the meanings of commands, so we should have the following equation:
\[
r_{move} = ([\![assume(x>0)]\!]\ \circ\ [\![x=x-1]\!]\ \circ\ r_{move}\ \circ\ [\![y=y+1]\!])\ \bigcup\ [\![assume(!(x>0))]\!]
\]
Denoting the right-hand side by  , we can write the above as
\[
, we can write the above as
\[
r_{move} = F(r_{move})
\]
Thus, the meaning of the procedure is the fixpoint of function  given by
\[
given by
\[
F(t) = ([\![assume(x>0)]\!]\ \circ\ [\![x=x-1]\!]\ \circ\ t\ \circ\ [\![y=y+1]\!])\ \bigcup\ [\![assume(!(x>0))]\!]
\]
Note that  is monotonic in its argument, because the operators
is monotonic in its argument, because the operators  ,
,  are monotonic:
are monotonic:
Similarly, the function is  -continuous (see Tarski's Fixpoint Theorem). Thus, it has the least fixpoint, and this fixpoint is given by
\[
-continuous (see Tarski's Fixpoint Theorem). Thus, it has the least fixpoint, and this fixpoint is given by
\[
r_{move} = \bigcup_{n \ge 0} F^n(\emptyset)
\]
In fact, 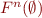 represents the result of inlining the recursive procedure
represents the result of inlining the recursive procedure  times. Therefore, if
times. Therefore, if 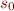 is the initial state such
that the computation in the procedure terminates within
is the initial state such
that the computation in the procedure terminates within  steps, then
steps, then  iff
iff  .
.
Multiple Mutually Recursive Procedures
The results extend to any number of call sites and any number of mutually recursive procedures, we just consider a function 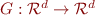 where
where  is the number of procedures; this mapping describes how, given one approximation of procedure semantics, compute a better approximation that is correct for longer executions. We have operations
is the number of procedures; this mapping describes how, given one approximation of procedure semantics, compute a better approximation that is correct for longer executions. We have operations  and
and  analogous to
analogous to  and
and  (indeed, the domain
(indeed, the domain  , that is
, that is  , is isomorphic to
, is isomorphic to 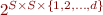 ).
).
The meaning of all procedures is therefore the tuple  given by
given by 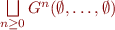 .
.
Remark:  is the least fixpoint of
is the least fixpoint of  , so by Tarski's Fixpoint Theorem, it is also the least
, so by Tarski's Fixpoint Theorem, it is also the least  such that
such that 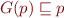 . Thus,
. Thus, 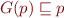 implies
implies  .
.
Example: Tree reversal.