Lattices
Definition: A lattice is a Partial order in which every two-element set has a least upper bound and a greatest lower bound.
Lemma: In a lattice every non-empty finite set has a lub ( ) and glb (
) and glb ( ).
).
Proof: is by induction!
Case where the set S has three elements x,y and z:
Let 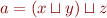 .
.
By definition of  we have
we have  and
and 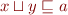 .
.
The we have again by definition of  ,
,  and
and  . Thus by transitivity we have
. Thus by transitivity we have  and
and  .
.
Thus we have  and a is an upper bound.
and a is an upper bound.
Now suppose that there exists  such that
such that  . We want
. We want  (a least upper bound):
(a least upper bound):
We have  and
and  , thus
, thus 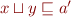 . But
. But  , thus
, thus 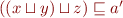 .
.
Thus  is the lub of our 3 elements set.
is the lub of our 3 elements set.
Lemma: Every linear order is a lattice.
If a lattice has least and greatest element, then every finite set (including empty set) has a lub and glb.
This does not imply there are lub and glb for infinite sets.
Example: In the oder 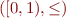 with standard ordering on reals is a lattice, the entire set has no lub.
The set of all rationals of interval
with standard ordering on reals is a lattice, the entire set has no lub.
The set of all rationals of interval ![Math $[0,10]$](/w/lib/exe/fetch.php?media=wiki:latex:/img8a7ad0389ab135687101f838d329f14f.png) is a lattice, but the set
is a lattice, but the set 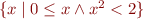 has no lub.
has no lub.
Definition: A complete lattice is a lattice where every set  of elemenbts has lub, denoted
of elemenbts has lub, denoted  , and glb, denoted
, and glb, denoted 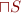 (this implies that there is top and bottom as
(this implies that there is top and bottom as 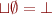 and
and 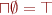 . This is because every element is an upper bound and a lower bound of
. This is because every element is an upper bound and a lower bound of  :
: 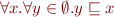 is valid, as well as
is valid, as well as 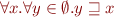 ).
).
Note: if you know that you have least upper bounds for all sets, it follows that you also have greatest lower bounds.
Proof: by taking the least upper bound of the lower bounds. Converse also holds, dually.
Example: Every subset of the set of real numbers has a lub. This is an axiom of real numbers, the way they are defined (or constructed from rationals).
Lemma: In every lattice,  .
.
Proof:
We trivially have 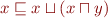 .
.
Let's prove that  :
:
 is an upper bound of
is an upper bound of  and
and  ,
, 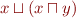 is the least upper bound of
is the least upper bound of  and
and  , thus
, thus  .
.
Definition: A lattice is distributive iff
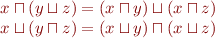
Example: Lattice of all subsets of a set is distributive. Linear order is a distributive lattice. See examples of non-distributive lattices in Distributive lattice and the characterization of non-distributive lattices.