Given a grammar, a concrete syntax tree is a directed tree with ordered children, given like this:

• leaves are labeled by terminals (tokens)
• internal nodes are labelled by non-terminals
  • if a node is labelled by non-terminal , then
    • there must be a production 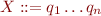such that
    • the children of the node are labelled by 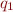, …, (in that order)
• root is the start symbol

Example grammar, with start symbol 'term':

term ::= factor | term "+" factor 
factor ::= INTLITERAL | IDENTIFIER

An example tree:

term(term(term(factor(IDENTIFIER("xx"))),
          "+",
          INTLITERAL(42)),
     "+",
     factor(IDENTIFIER("yy"))

This tree shows that

xx + 42 + yy

can be generated by the grammar.

The yield of the concrete syntax tree is the sequence of terminals that we obtain by traversing the tree in infix order.

The parse tree “proves” that the yield can be generated by the grammar.

Parse tree is more abstract than derivation: there are several derivation that result in the same concrete syntax tree, depending on the order in which we expand the non-terminals.

These trees typically ignore simple tokens such as

• keywords
• parentheses
• operator symbols

Instead, the names of syntax tree nodes and their content carry sufficient information

abstract class Expression
case class IntegerLiteral(v : Int) extends Expressioon
case class Variable(id : String) extends Expression
case class Plus(e1 : Expression, e2 : Expression) extends Expression
case class Minus(e1 : Expression, e2 : Expression) extends Expression

The order of operators in AST determines the meaning. Compare:

Minus(Minus(100,20),5)   --> 75
Minus(100,Minus(20,5))   --> 85

Must be careful to ensure the desired priority and the order of application of operators.

left-associative operators:

def parseTerm : Expression = {
  var e = parseFactor
  while (lex.token = MINUS) {
    lex.next
    e = Minus(e, parseFactor)
  }
  e
}

right-associative operator:

def parseTerm : Expression = {
  val e1 = parseFactor
  if (lex.token = EXPONENT) {
    lex.next
    val e2 = parseTerm
    Exponent(e1,e2)
  } else {
    e1
  }
}