Type Checking Let and Letrec
Let Expressions
Expression
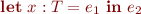
can be viewed as a shorthand for

because they both evaluate to ![Math $e_2[x:=e_1]$](/w/lib/exe/fetch.php?media=wiki:latex:/img50e67670a1dd41b877db67cb5a346936.png)
From this follows the type rule for let expressions:
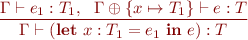
Example: We can represent non-recursive method definitions using let
In this Java-like code
int f(int x) { return x + 3; } int main(int y) { return f(f(y+5)); }
the main function can be type checked by type checking
let (f:int->int) = % x:int. x+3 in %y:int. f(f(y+5))
Recursive Let (letrec) Expressions
How to represent recursive definitions in lambda calculus? Consider this example
int g(int x) { return (x <= 0 ? 1 : (x+g(x-1))); } int h(int x) { return g(h(x)); } expr
We use recursive version of let, denoted letrec, representing above as
letrec (g : int->int) = (ite (<= x 0) 1 (+ x (g (- x 1)))) and (h : int->int) = (g (h x)) in expr
Type rule for letrec:
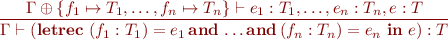
Example: type check the previous code using the letrec rule.
Using Lambda Calculus and Letrec
- describes type checking of mutually recursive definitions
- result is again expression: supports nested function definitions
- each of
 ,
,  can contain other letrec expressions
can contain other letrec expressions