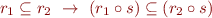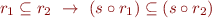Relational Semantics of Procedures
Let  be the set of states and
be the set of states and  denote
denote 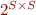 , the set of all relations on
, the set of all relations on  .
.
In Relational Semantics for a language without procedures we had semantic function that maps programs to relations

so 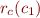 was the relation corresponding to the command
was the relation corresponding to the command  , and we denote it by
, and we denote it by ![Math $[\![c_1]\!]$](/w/lib/exe/fetch.php?media=wiki:latex:/img221f53b47ce4a0fa85fbc98feaac35d1.png) .
.
How can we define semantics for program with recursive procedures?
We consider first the case of procedures without parameters; adding parameters is straightforward.
One Recursive Procedure
We first illustrate the semantics for one recursive procedure. The definition only relies on the Lattices structure, so it generalizes to recursive definitions with multiple procedures, and recursive definitions in general.
Example: Consider the following procedure that, if  are positive, moves the content of x into y.
are positive, moves the content of x into y.
var x,y;
proc move() {
if (x > 0) {
x = x - 1;
move();
y = y + 1;
}
}
or, expressed using non-deterministic choice and assume:
var x,y;
proc move() {
( assume(x>0);
x = x - 1;
move();
y = y + 1;
)
[] (assume (!(x>0))
}
Suppose we have relation  describing the meaning of the procedure. By Relational Semantics, this procedure should behave similarly as the meanings of commands, so we should have the following equation:
describing the meaning of the procedure. By Relational Semantics, this procedure should behave similarly as the meanings of commands, so we should have the following equation:
![Equation \begin{equation*}
r_{move} = ([\![assume(x>0)]\!]\ \circ\ [\![x=x-1]\!]\ \circ\ r_{move}\ \circ\ [\![y=y+1]\!])\ \bigcup\ [\![assume(!(x>0))]\!]
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imgf5991873497e69c2c02074dff4c1e67b.png)
Denoting the right-hand side by  , we can write the above as
, we can write the above as
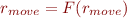
Thus, the meaning of the procedure is the fixpoint of function  given by
given by
![Equation \begin{equation*}
F(t) = ([\![assume(x>0)]\!]\ \circ\ [\![x=x-1]\!]\ \circ\ t\ \circ\ [\![y=y+1]\!])\ \bigcup\ [\![assume(!(x>0))]\!]
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img89ca46b27b5953bcb37f062b7e2a3d47.png)
Note that  is monotonic in its argument, because the operators
is monotonic in its argument, because the operators  ,
,  are monotonic:
are monotonic:
Similarly, the function is  -continuous (see Tarski's Fixpoint Theorem). Thus, it has the least fixpoint, and this fixpoint is given by
-continuous (see Tarski's Fixpoint Theorem). Thus, it has the least fixpoint, and this fixpoint is given by
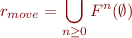
In fact, 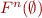 represents the result of inlining the recursive procedure
represents the result of inlining the recursive procedure  times. Therefore, if
times. Therefore, if  is the initial state such
that the computation in the procedure terminates within
is the initial state such
that the computation in the procedure terminates within  steps, then
steps, then  iff
iff  .
.
In this example, we have
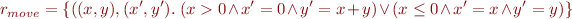
Multiple Mutually Recursive Procedures
Example: Consider the following example. The idea is that after execution of the procedure even(), the boolean variable wasEven shows whether the initial value of x was even.
var x : int
var wasEven : bool
proc even() {
if (x==0) {
wasEven = true;
} else {
x = x - 1;
odd();
}
}
proc odd() {
if (x==0) {
wasEven = false;
} else {
x = x - 1;
even();
}
}
We can write the bodies as follows:
even() = (assume(x==0); wasEven = true) [] (assume(x!=0); x = x - 1; odd()) odd() = (assume(x==0); wasEven = false) [] (assume(x!=0); x = x - 1; even())
Now, we turn mutually recursive definition into a simple recursive definition by taking the pair of the meaning of odd and even. We need to find
relations  ,
,  such that
such that

where the function 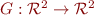 is given by:
is given by:
![Equation \begin{equation*}
G(E,O) =
\begin{array}[t]{@{}l@{}}
\bigg( ([\![assume(x==0)]\!] \circ [\![wasEven=true]\!]) \cup
([\![assume(x!=0)]\!] \circ [\![x=x-1]\!] \circ O)\ , \\
([\![assume(x==0)]\!] \circ [\![wasEven=false]\!]) \cup
([\![assume(x!=0)]\!] \circ [\![x=x-1]\!] \circ E) \bigg)
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img2839b60a62e8dcf09f7868fc3040afac.png)
We define lattice structure on  by
by
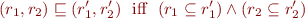
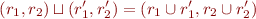
Note that:
![Equation \begin{equation*}
G(\emptyset,\emptyset) = ([\![assume(x==0)]\!] \circ [\![wasEven=true]\!], [\![assume(x==0)]\!] \circ [\![wasEven=false]\!])
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img7ff74ef2bb74f9d85300e7155f21f4b6.png)
![Equation \begin{equation*}
G(G(\emptyset,\emptyset)) =
\begin{array}[t]{@{}l@{}}
\bigg( ([\![assume(x==0)]\!] \circ [\![wasEven=true]\!]) \cup
([\![assume(x!=0)]\!] \circ [\![x=x-1]\!] \circ G(\emptyset,\emptyset).\_2)\ , \\
([\![assume(x==0)]\!] \circ [\![wasEven=false]\!]) \cup
([\![assume(x!=0)]\!] \circ [\![x=x-1]\!] \circ G(\emptyset,\emptyset).\_1) \bigg)
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img3a402770259f6eeb0d41c73cba2d9864.png)
where 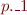 and
and 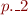 denote first, respectively, second, element of the pair
denote first, respectively, second, element of the pair  .
.
The results extend to any number of call sites and any number of mutually recursive procedures, we just consider a function 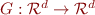 where
where  is the number of procedures; this mapping describes how, given one approximation of procedure semantics, compute a better approximation that is correct for longer executions.
is the number of procedures; this mapping describes how, given one approximation of procedure semantics, compute a better approximation that is correct for longer executions.
We define  and
and  analogous to
analogous to  and
and  (indeed, the domain
(indeed, the domain  , that is
, that is  , is isomorphic to
, is isomorphic to 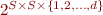 ).
).
The meaning of all procedures is then the tuple  given by
given by 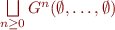 .
.
Example
In the example above, we can prove that
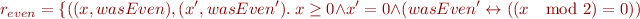
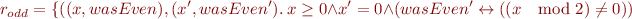
Remark
 is the least fixpoint of
is the least fixpoint of  , so by Tarski's Fixpoint Theorem, it is also the least
, so by Tarski's Fixpoint Theorem, it is also the least  such that
such that 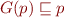 . Thus,
. Thus, 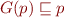 implies
implies  .
.