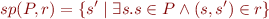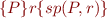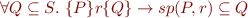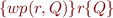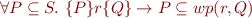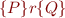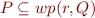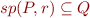Hoare Logic
Hoare logic is a way of inserting annotations into code to make proofs about program behavior simpler.
Example Proof
//{0 <= y} i = y; //{0 <= y & i = y} r = 0; //{0 <= y & i = y & r = 0} while //{r = (y-i)*x & 0 <= i} (i > 0) ( //{r = (y-i)*x & 0 < i} r = r + x; //{r = (y-i+1)*x & 0 < i} i = i - 1 //{r = (y-i)*x & 0 <= i} ) //{r = x * y}
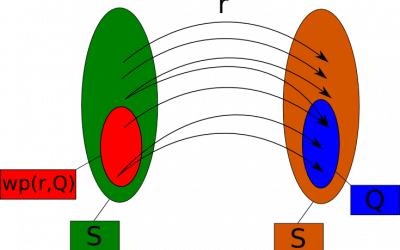
Hoare Triple for Sets and Relations
When 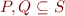 (sets of states) and
(sets of states) and 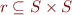 (relation on states, command semantics) then
Hoare triple
(relation on states, command semantics) then
Hoare triple
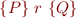
means
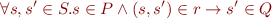
We call  precondition and
precondition and  postcondition.
postcondition.
Note: weakest conditions (predicates) correspond to largest sets; strongest conditions (predicates) correspond to smallest sets that satisfy a given property (Graphically, a stronger condition 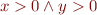 denotes one quadrant in plane, whereas a weaker condition
denotes one quadrant in plane, whereas a weaker condition  denotes the entire half-plane.)
denotes the entire half-plane.)
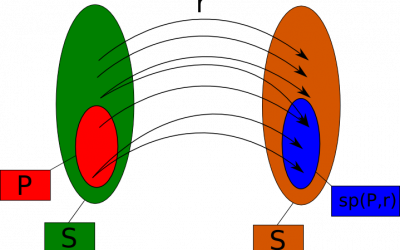
Strongest Postcondition - sp
Lemma: Characterization of sp
 is the the smallest set
is the the smallest set  such that
such that 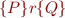 , that is:
, that is:
Weakest Precondition - wp
Definition: for  ,
, 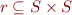 ,
,
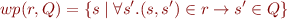
Note that this is in general not the same as 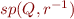 when relation is non-deterministic.
when relation is non-deterministic.
Lemma: Characterization of wp
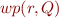 is the largest set
is the largest set  such that
such that 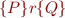 , that is:
, that is:
Some More Laws on Preconditions and Postconditions
We next list several more lemmas on properties of wp, sp, and Hoare triples.
Postcondition of inverse versus wp
If instead of good states we look at the completement set of “error states”, then  corresponds to doing
corresponds to doing 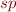 backwards. In other words, we have the following:
backwards. In other words, we have the following:
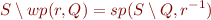
Disjunctivity of sp
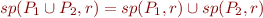
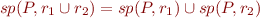
Conjunctivity of wp
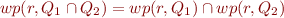
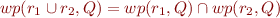
Pointwise wp
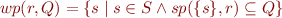
Pointwise sp
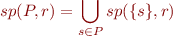
Three Forms of Hoare Triple
The following three conditions are equivalent:
Hoare Triples, Preconditions, Postconditions on Formulas and Commands
Let  and
and  be formulas in our language
be formulas in our language  (see simple programming language). We define Hoare triples on these syntactic entities by taking their interpretation as sets and relations:
(see simple programming language). We define Hoare triples on these syntactic entities by taking their interpretation as sets and relations:
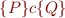
means
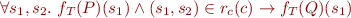
In words: if we start in a state satisfying  and execute
and execute  , we obtain a state satisfying
, we obtain a state satisfying  .
.
We then similarly extend the notion of  and
and 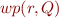 to work on formulas and commands. We use the same notation and infer from the context whether we are dealing with sets and relations or formulas and commands.
to work on formulas and commands. We use the same notation and infer from the context whether we are dealing with sets and relations or formulas and commands.
Composing Hoare Triples
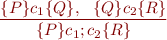
We can prove this from
- definition of Hoare triple
- meaning of ';' as

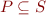 ,
,