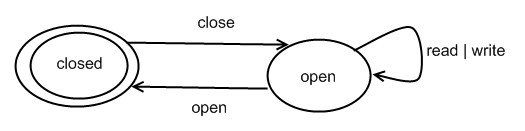
Model Checking Finite-State Systems
Suppose we have a finite state system given by an automaton  , compile the specification into an automaton
, compile the specification into an automaton  and check
and check 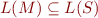 , that is
, that is
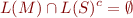
that is, check that the product of automata  and
and  accepts no strings (each string would be a counterexample).
accepts no strings (each string would be a counterexample).
Some of the operations that we can do on specifications:
- for specifications given by formulas: all operations that we can do on formulas (
 ,
,  ,
,  ,
,  ,
,  , temporal operators, …)
, temporal operators, …) - we can also 'ignore' certain parts of the alphabet
Ignoring Actions Irrelevant for Spec
Suppose we have specification
(open (read+write)* close)*
but our language is as in the Example with Procedures, so it contains many other actions (startLog, endLog, p1Start, p1End, …)
Theorem:
Let 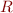 be a regular language in alphabet
be a regular language in alphabet  and
and 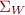 be a disjoint alphabet. Define
be a disjoint alphabet. Define
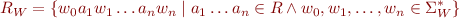
Then 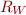 is also a regular.
is also a regular.
Limitations of Finite State Machines
One possibility is to treat procedure calls as gotos.
This corresponds to approximating context-free language of the procedure with a regular one - union of control-flow graphs.
- logging can be either on or off in readContent procedure of Example with Procedures
- this would result in false warnings