Deciding Quantifier-Free FOL over Ground Terms
Instead of considering arbitrary interpretations, consider now satisfiability over an interpretation of ground terms.
For now also no relation symbols.
What is the difference compared to models considered in Deciding Quantifier-Free FOL?
Can we treat variables as constants in this case?
Is the following formula satisfiable ?
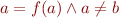
And the following ?

Axioms for Term Algebras
Term algebra axioms for function symbols (recall Unification):
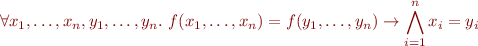
and
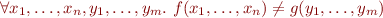
for  and
and  distinct symbols.
distinct symbols.
Unless the language is infinite, we have that each element is either a constant or is result of application of some function symbols:
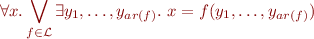
Additional axiom schema for finite terms:
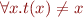
if 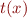 is a term containing
is a term containing  but not identical to
but not identical to  .
.
Unification as Decision Procedure
Represent each disequation 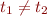 as
as
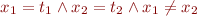
where 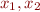 are fresh variables.
are fresh variables.
Unification represents the set of all solutions of positive literals.
If the mgu does not have same values for  and
and  , then there is a ground substitution that assigns
, then there is a ground substitution that assigns  and
and  different ground terms. More generally,
different ground terms. More generally,
Theorem: Let  be a set of equations and disequations where disequations are only between variables. Let
be a set of equations and disequations where disequations are only between variables. Let 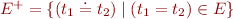 the unification problem for equations in
the unification problem for equations in  . Then
. Then
- if
 has no unifier, the set
has no unifier, the set  is unsatisfiable over ground terms;
is unsatisfiable over ground terms; - if
 has a most general unifier
has a most general unifier  such that for all
such that for all 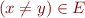 we have
we have  , then if the language contains at least one function symbol of arity at least one (i.e. the set of ground terms is infinite) then
, then if the language contains at least one function symbol of arity at least one (i.e. the set of ground terms is infinite) then  is satisfiable.
is satisfiable.
Note: we need assumption that there are infinitely many terms, consider for example 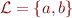 and formula
and formula  .
.
Algorithmic Aspects
We can use DAGs and union-find as well.
The result is similar to checking satisfiability of ground formulas over arbitrary interpretations (but e.g. 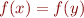 implies
implies  ).
).
Selector Symbols
They are useful for avoiding the need for variables.
We represent 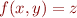 by
by 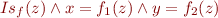
const/car/cdr: one binary function symbol, cons
Represent 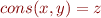 by
by
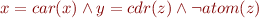
here
 is negation of
is negation of 
 is
is 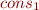
 is
is 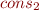 .
.
Notes on Decidability
For quantifier-free formulas, satisfiability is decidable, whether or not we have predicate symbols as well.
Let us clarify the status of quantified constraints.
In Herbrand interpretation we interpret functions and constants as themselves (their interpretation is fixed) but we interpret predicates as arbitrary predicates on ground terms.
So, for quantified case:
- if we have no predicates: theory is decidable, using quantifier elimination (these structures are called “term algebras”, see List of Theories Admitting QE)
- if we have predicates: this is satisfiability in Herbrand models, equivalent to satisfiability in FOL without equality, so it is undecidable
References
- On the Theory of Structural Subtyping, see proof of Lemma 25 on page 13
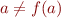 ).
).