Quotient of an Interpretation under a Congruence
Example: quotient on pairs of natural numbers
Let 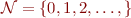 . Consider a structure with domain
. Consider a structure with domain  , with functions (plus and minus):
, with functions (plus and minus):
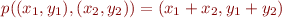
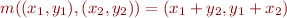
Relation  defined by
defined by
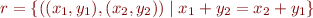
is a congruence with respect to operations  and
and  . Indded, we can check that, for example, if
. Indded, we can check that, for example, if 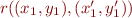 and
and
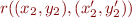 then
then
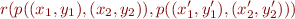
Congruence is an equivalence relation. What are equivalence classes for elements:
Whenever we have a congruence in an interpretation, we can shrink the structure to a smaller one by merging elements that are in congruence.
In the resulting structure ![Math $([N^2], I_Q)$](/w/lib/exe/fetch.php?media=wiki:latex:/imge1eb6e9867135f1179496cc7a74f7b95.png) we define operations
we define operations  and
and  such that the following holds:
such that the following holds:
![Equation \begin{equation*}
\begin{array}{l}
I_Q(p)( [(x_1,y_1)] , [(x_2,y_2)] ) = [(x_1 + x_2, y_1 + y_2)] \\
I_Q(m)( [(x_1,y_1)] , [(x_2,y_2)] ) = [(x_1 + y_2, y_1 + x_2)]
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imgdaea4e70ba8d3c8c582d0ee67ddcc970.png)
This construction is an algebraic approach to construct from natural numbers one well-known structure. Which one?
Note: this construction can be applied whenever we have an associative and commutative operation  satisfying the cancelation law
satisfying the cancelation law  . It allows us to construct a structure where operation
. It allows us to construct a structure where operation  has an inverse. What do we obtain if we apply this construction to multiplication of strictly positive integers?
has an inverse. What do we obtain if we apply this construction to multiplication of strictly positive integers?
Definition of Quotient of an Interpretation
(Recall notation in First-Order Logic Semantics.)
Let 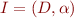 be an interpretation of language
be an interpretation of language  with
with 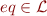 for which Axioms for Equality hold, that is,
for which Axioms for Equality hold, that is, 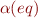 is a congruence relation for
is a congruence relation for  . We will construct a new model
. We will construct a new model  .
.
For each element  , define
, define
![Equation \begin{equation*}
[x] = \{ y \mid (x,y) \in \alpha(eq) \}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imge81b73ef8de708f4121476d625c314bd.png)
Let
![Equation \begin{equation*}
[D] = \{ [x] \mid x \in D \}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img3f90555cc93a3f53350e21e6376203f4.png)
The constructed model will be ![Math $I_Q = ([D],\alpha_Q)$](/w/lib/exe/fetch.php?media=wiki:latex:/img0fb77e30d3ba35dd5bb43f7dc8ed22a6.png) where
where
![Equation \begin{equation*}
\alpha_Q(R) = \{ ([x_1],\ldots,[x_n]) \mid (x_1,\ldots,x_n) \in \alpha(R) \}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img23fe519846fb8db360ebf3cbde0371a4.png)
In particular, when  is
is  we have
we have
Functions are special case of relations:
![Equation \begin{equation*}
\alpha_Q(f) = \{ ([x_1],\ldots,[x_n],[x_{n+1}]) \mid (x_1,\ldots,x_n,x_{n+1}) \in \alpha(f) \}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img87580c0cbf20e4249e9e642a2d126b28.png)
Interpretation of variables is analogous to interpretation of constants:
![Equation \begin{equation*}
\alpha_Q(x) = [\alpha(x)]
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img41226f66b61ed04b4b4c4eae00154f33.png)
Lemma 0: For all 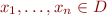 ,
,
![Equation \begin{equation*}
([x_1],\ldots,[x_n]) \in \alpha_Q(R) \mbox{ iff } (x_1,\ldots,x_n) \in \alpha(R)
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img5f3c5a6027e5c3e8d80b9d6458ed83c4.png)
Lemma 1: For each function symbol  with
with 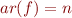 , the relation
, the relation 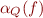 is a total function
is a total function ![Math $[D]^n \to [D]$](/w/lib/exe/fetch.php?media=wiki:latex:/img24e2ec4aae146309317d72060f3465be.png) and for all
and for all 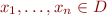 ,
,
![Equation \begin{equation*}
\alpha_Q(f)([x_1],\ldots,[x_n]) = [\alpha(f)(x_1,\ldots,x_n)]
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img832ebed329208fd475c04a09c3e13509.png)
Lemma 2: For each term  we have
we have ![Math $e_T(t)(I_Q) = [e_T(t)(I)]$](/w/lib/exe/fetch.php?media=wiki:latex:/img55e15b4ba80e81d38ae08e3ce7913cdc.png) .
.
Theorem: For each formula  that contains no '=' symbol, we have
that contains no '=' symbol, we have 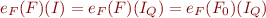 where
where 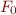 is result of replacing 'eq' with '=' in
is result of replacing 'eq' with '=' in  .
.
![Math $[(1,1)] = $](/w/lib/exe/fetch.php?media=wiki:latex:/img59f2c025571202402b85a56c98961149.png)
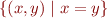
![Math $[(10,1)] = $](/w/lib/exe/fetch.php?media=wiki:latex:/img14c2772767fefb80edd6e518e928c97b.png)
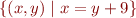
![Math $[(1,10)] = $](/w/lib/exe/fetch.php?media=wiki:latex:/imgd9d71cde6070a9a5af893a771ac75f2d.png)
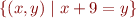
 where
where  is the set of integers.
is the set of integers. 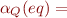
![Math $\{ ([x_1],[x_2]) \mid (x_1,x_2) \in \alpha(eq) \} = \{ (a,a) \mid a \in D \}$](/w/lib/exe/fetch.php?media=wiki:latex:/img27eb4d986fe3e5906b0270ef56bacdff.png) that is, the interpretation of eq in
that is, the interpretation of eq in ![Math $([D],I_Q)$](/w/lib/exe/fetch.php?media=wiki:latex:/img50364968dfa74d52fb982153ab6771c7.png) is diagonal relation - equality.
is diagonal relation - equality.