Lecture 9: Fixpoints in static analysis
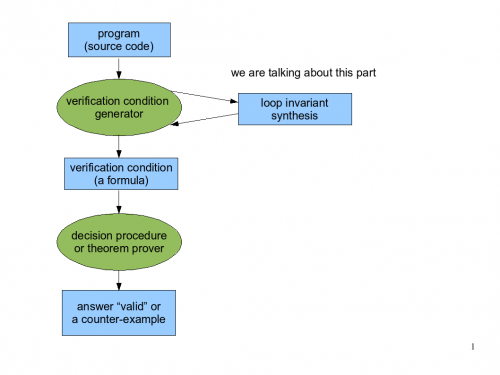
Recall formula propagation from Lecture 7. See correctness of formula propagation.
Static analysis as equation solving in a lattice
If instead of formulas as 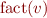 we have elements of some lattice, this condition becomes
we have elements of some lattice, this condition becomes
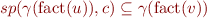
(where sp in now denotes operator on states and not formulas).
By properties of Galois connection, this is equivalent to
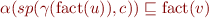
and we defined best transformer as 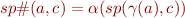 , so this condition is equivalent to
, so this condition is equivalent to
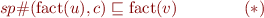
We conclude that finding an inductive invariant expressed using elements of a lattice corresponds to finding a solution to a system of inequations  for all
for all 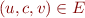 . We next examine the existence and computation of such solutions more generally.
. We next examine the existence and computation of such solutions more generally.
Note that 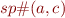 is a function monotonic in a. Why?
is a function monotonic in a. Why?
So, we are solving a conjunction of inequations
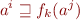
where  are variables ranging over a lattice
are variables ranging over a lattice  (one for each control-flow graph node), and
(one for each control-flow graph node), and  are monotonic functions on
are monotonic functions on  (one for each edge in the control-flow graph).
(one for each edge in the control-flow graph).
From a system of equations to one equation
In lattice, we have that a conjunction of inequations
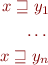
is equivalent to 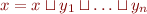 (
( is least upper bound of them).
is least upper bound of them).
So we can write the conjunction of inequations in the previous section as a system of equations
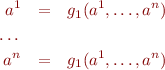
Now, introduce a new product lattice 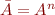 with order
with order
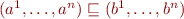 iff
iff 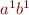 ,\ldots,
,\ldots,  all hold. Then we have reduced the problem to finding a solution to equation
all hold. Then we have reduced the problem to finding a solution to equation
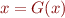
where  . Function
. Function  is also monotonic.
is also monotonic.
The solution of equation of the form 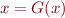 is called a fixed point of function
is called a fixed point of function  , because
, because  leaves
leaves  in place.
in place.
The iterative process that we described above corresponds to picking an initial element  such that
such that  and then computing
and then computing 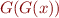 , \ldots,
, \ldots, 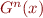 .
.
- we have

- we have

If it stabilizes we have 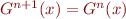 , so
, so 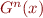 is a fixed point. This always happens if there are no infinite ascending chains.
is a fixed point. This always happens if there are no infinite ascending chains.
What is we have arbitrary lattices? See, for example non-converging iteration in reals.
 -continuity in a complete lattice is a requirement that for every chain
-continuity in a complete lattice is a requirement that for every chain  we have
we have
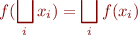
(generalizes continuity in real numbers). For continuous functions, even if there are infinite ascending chains, the fixed point iteration converges in the limit.
In general, even without  -continuity we know that the fixed point exists, due to Tarski fixed point theorem.
-continuity we know that the fixed point exists, due to Tarski fixed point theorem.
See also lecture notes in SAV07 resource page, in particular notes by Michael Schwartzbach for the finite case and slides by David Schmidt for  -continuity.
You can also check papers by Cousot & Cousot:
-continuity.
You can also check papers by Cousot & Cousot:
Widening
When a lattice has infinite ascending chain property, applying the strongest postcondition for each program point need not converge.
- Example: interval analysis
One approach: redesign the lattice to make it have no infinite ascending chain
Another approach: change the fixpoint iteration itself so that it goes faster - widening.
The effect is as if we had a lattice with smaller height (but that still covers everything from  to
to  ) and this lattice is overlayed on top of the bigger lattice.
) and this lattice is overlayed on top of the bigger lattice.
Example (Michael Swartzbach's notes, Section 7): define widening using a monotone operator  that is composed with the fixpoint operator
that is composed with the fixpoint operator  . The resulting composition is again monotone and the result is similar to computing in a smaller lattice.
. The resulting composition is again monotone and the result is similar to computing in a smaller lattice.
Example widening operator: take finite set B of bounds such that  . Usually
. Usually  also contains some constants that occur in the program. Then jump to the closest lower and upper bounds. The value can jump only finitely many times before reaching
also contains some constants that occur in the program. Then jump to the closest lower and upper bounds. The value can jump only finitely many times before reaching ![Math $[-\infty,+\infty]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgb4adf0b8ef783638901d0ebe43bbf68c.png) , but often the fixpoint can be reached before this happens.
, but often the fixpoint can be reached before this happens.
Sometimes we first use  for fixpoint iteration until we conclude that the value at some program point is not “stable” (it has not converged yet), and then we switch to
for fixpoint iteration until we conclude that the value at some program point is not “stable” (it has not converged yet), and then we switch to
- advantage: more precise
- drawback: not monotonic (example), so more difficult to reason about
Often the operator is defined not just on the current fact  but as a binary operator that takes
but as a binary operator that takes  and
and 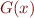 , denoted
, denoted 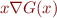 , with property
, with property  .
.
Narrowing
Once we have reached above the fixpoint (using widening or anything else), we can always apply the fixpoint operator  and improve the precision of the results.
and improve the precision of the results.
If this is too slow, we can stop at any point or use a narrowing operator, the result is sound.
Instead of using the fixpoint operator  , we can use any operator that leaves our current value above fixpoint.
, we can use any operator that leaves our current value above fixpoint.
See Combination of Abstractions in ASTREE, Section 8.1, define  such that
such that 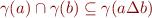
- example: take
 as
as  , or even some improved version
, or even some improved version
Reduced product
When we have multiple lattices for different properties, we can of course run both analyses independently.
If the analyses do not exchange information the result is same as running them one after the other - this corresponds to taking product of two lattices and operations on them.
To obtain more precise results, we allow analyses to exchange information.
Reduced product: Systematic Design of Program Analysis Frameworks, Section 10.1.
Key point: define  by
by
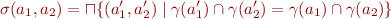
The function  improves the precision of the element of the lattice without changing its meaning. Subsequent computations with these values then give more precise results.
improves the precision of the element of the lattice without changing its meaning. Subsequent computations with these values then give more precise results.