Tarski's fixed point theorem
A complete lattice is a lattice where every set of elements  has the least upper bound
has the least upper bound  and the greatest lower bound
and the greatest lower bound 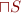 (this implies that there is top and bottom as
(this implies that there is top and bottom as 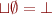 and
and 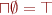 .
.
(Note: if you know that you have least upper bounds for all sets, it follows that you also have greatest lower bounds, by taking the least upper bound of the lower bounds. Converse also holds, dually.)
Let 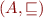 be a complete lattice and
be a complete lattice and 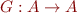 a monotonic function.
a monotonic function.
Define
 the set of postfix points of
the set of postfix points of  (e.g.
(e.g.  is a postfix point)
is a postfix point)
 the set of fixed points of
the set of fixed points of  . Note that
. Note that  .
.
Theorem: Let  . Then
. Then  is the least element of
is the least element of  .
.
Proof is amusing. Let  range over elements of
range over elements of  .
.
- applying monotonic
 from
from  we get
we get 
- so
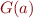 is a lower bound on
is a lower bound on  , but
, but  is the greatest lower bound, so
is the greatest lower bound, so 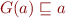
- therefore

 is closed under
is closed under  , by monotonicity, so
, by monotonicity, so 
 is a lower bound on
is a lower bound on  , so
, so 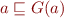
- from
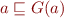 and
and 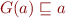 we have
we have 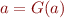 , so
, so 
 is a lower bound on
is a lower bound on  so it is also a lower bound on a smaller set
so it is also a lower bound on a smaller set 
Dually, if  the set of prefix points of
the set of prefix points of  , then
, then  is the largest element of
is the largest element of  .
.
Tarski's Fixed Point theorem shows that in a complete lattice with a monotonic function  on this lattice, there is at least one fixed point of
on this lattice, there is at least one fixed point of  , namely the least fixed point
, namely the least fixed point  .
.
To find this fixed point, we can start from  . Then the sequence
. Then the sequence  will converge to the least fixed point if
will converge to the least fixed point if  is
is  -continuous, i.e. if
-continuous, i.e. if 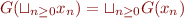 .
.
In order to converge faster, we can use techniques such as widening.
More information: