Simply Typed Lambda Calculus
Lambda calculus is a simple and powerful notation for defining functions. Among its uses are
- foundation of programming languages, especially functional languages such as Ocaml, Haskell, and Scala
- basis of higher order logic
In lambda calculus, functions have no side effects
- they are mathematical functions from arguments to results
- this model is appropriate for type checking rules, because types do not change over time
- lambda calculus also supports higher-order functions
Anonymous Functions in Lambda Calculus
A function which takes its argument and increments it by 2 is given by lambda expression  . The
. The  operator is a binder used to indicate that a variable is to be treated as an argument of a function. We indicate function application by juxtaposition, writing
operator is a binder used to indicate that a variable is to be treated as an argument of a function. We indicate function application by juxtaposition, writing 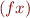 instead of
instead of 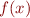 . Here are some example expressions and their values:
. Here are some example expressions and their values:
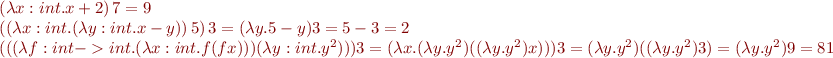
Concrete syntax for  :
:
Lambda Expressions
Abstract syntax of untyped lambda expressions:
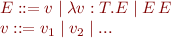
That is, an expression is 1) a variable, 2) a lambda expression defining a function, or 3) an application of one expression to another.
Certain predefined variables are called constants (e.g. 7, 42, 13, but also operations +, *).
Types are given by the following grammar:
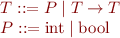
There can be additional primitive types  .
.
Currying
Instead of
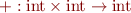
we have
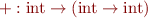
Therefore  is a function that increments its argument by
is a function that increments its argument by 
- expression
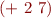 is just a shorthand for
is just a shorthand for 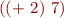
This is called currying in the honor of Haskell Curry
In general, instead of function
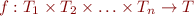
we can use function
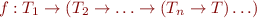
Beta Reduction
The main rule of lambda calculus is beta reduction, which formalizes function application:
![Equation \begin{equation*}
(\lambda x. e_1) e_2 = e_1[x:=e_2]
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img642b7cbc7c3af1229e5b16771cef8844.png)
Here we assume capture-avoiding substitution
- we do renaming to avoid name clashes
Example:
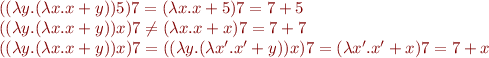
Rules for Constants
For each constant we have appropriate rule, for example we have
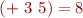
and so on, for each pair of integer constants. Similarly,
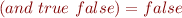
we can introduce conditional constant  , writing
, writing  , with rules
, with rules
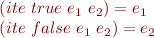
and so on.
If we get something like
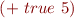
this is a run-time type error
- program would crash at run-time or produce bad result
- we introduce a type system to avoid this
Type Rules
Environment  maps variable names to types
maps variable names to types
Variable
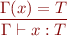
Application
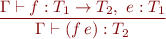
Abstraction
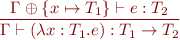
Example: if % denotes  , type check lambda expression
, type check lambda expression
(%f:int->int. (%x:int. f(f x))) ({+} 8)
in environment 
Let Expressions
Expression
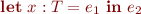
can be viewed as a shorthand for

because they both evaluate to ![Math $e_2[x:=e_1]$](/w/lib/exe/fetch.php?media=wiki:latex:/img50e67670a1dd41b877db67cb5a346936.png)
From this follows the type rule for let expressions:
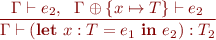
Example: We can represent non-recursive method definitions using let
In this Java-like code
int f(int x) {
return x + 3;
}
int main(int y) {
return f(f(y+5));
}
the main function can be type checked by type checking
let f = % x:int. x+3 in
%y:int. f(f(y+5))
<code>
===== Recursive Let (letrec) Expressions =====
How to represent recursive definitions in lambda calculus? Consider this example
<code>
int g(int x) {
return (x <= 0 ? 1 : (x+g(x-1)));
}