Simply Typed Lambda Calculus
A restriction of Untyped Lambda Calculus to type terms that has simpler semantics.
- foundation of modern functional programming languages (when extended with recursion)
- particularly suitable as a foundation of logic: due to termination properties
Simple Types
Consider a family of base types  .
.
The set of simple types are defined by grammar
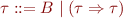
The type  is meant to denote functions from
is meant to denote functions from  to
to  (whether it denotes total or partial or computable functions, depends on particular semantics).
(whether it denotes total or partial or computable functions, depends on particular semantics).
In simply typed lambda calculus, each variable is assigned one type from  .
.
Syntax of System with Concrete Types
Given a family of base types, a term  of simply typed lambda calculus is like a term of Untyped Lambda Calculus, but carries a type. We define it as follows:
of simply typed lambda calculus is like a term of Untyped Lambda Calculus, but carries a type. We define it as follows:
- variable of type
 is a term of type
is a term of type 
- if
 has type
has type  and
and  is a variable of type
is a variable of type  , then
, then  is a term of type
is a term of type 
- if
 is a term of type
is a term of type  and
and  is a term of type
is a term of type  , then
, then 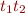 is a term of type
is a term of type 
Notation using type rules:
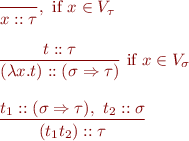
Note that there is no way to assign a type to  such that the term
such that the term  is well typed. Therefore,
is well typed. Therefore,  is not a term of simply typed lambda calculus.
is not a term of simply typed lambda calculus.
Hindley-Milner Type Inference
Hindley-Milner type inference uses unification to infer possible types of lambda terms, even if we do not specify types for variables. The problem reduces to unification in language that has as many constants as there are base types, and one binary constructor (function constructor).
In some cases, such as  , there is an infinite family of possible concrete types. In such cases, Hindley-Milner inference computes the most-general unifier of constraints, which gives polymorphic type. For simplicity we assume that we have obtained some concrete types for variables and therefore for lambda terms.
, there is an infinite family of possible concrete types. In such cases, Hindley-Milner inference computes the most-general unifier of constraints, which gives polymorphic type. For simplicity we assume that we have obtained some concrete types for variables and therefore for lambda terms.
Strong Normalization
Unlike beta reduction on typed terms, beta reduction on typed terms always terminates and the result does not depend on the order of applying beta reductions in the term. (Proof requires some work, and there are several variants; there are some short and elegant proofs that interpret based on set theory, see Barendregt's chapter.)
The consequence is that for each term in simply typed lambda calculus we can compute a normal form where all beta reductions were applied.