Untyped Lambda Calculus
Lambda calculus is a simple and powerful notation for defining functions. Among its uses are
- foundation of programming languages, especially functional languages such as Ocaml, Haskell, and Scala
- basis of higher order logic
Intuition
A function which takes its argument and increments it by 2 is given by lambda expression  . The
. The  operator is a binder used to indicate that a variable is to be treated as an argument of a function. We indicate function application by juxtaposition. Here are some example expressions and their values:
operator is a binder used to indicate that a variable is to be treated as an argument of a function. We indicate function application by juxtaposition. Here are some example expressions and their values:
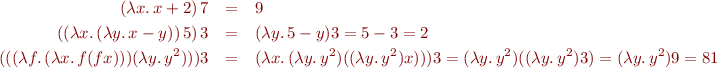
Concrete syntax for  :
:
Lambda expressions
Untyped lambda expressions are given by following grammar:
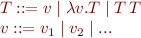
That is, an expression is a variable, a lambda expression defining a function, or an application of one expression to another.
Beta reduction
The main rule of lambda calculus is beta reduction, which formalizes function application:
![Equation \begin{equation*}
(\lambda x.\, s) t\ \mathop{\to}\limits^{\beta}\ s[x:=t]
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img2b61455233f44e88110b5f778b72c7a1.png)
where we assume capture-avoiding substitution. In general, we identify terms that differ only by renaming of fresh bound variables.
Here  is a binary 'reduction' relation on terms. We build larger relations on terms by
is a binary 'reduction' relation on terms. We build larger relations on terms by
- performing reduction in any context
 , so we have
, so we have ![Math $C[(\lambda x.\, s) t]\ \mathop{\to}\limits^{\beta}\ C[s[x:=t]]$](/w/lib/exe/fetch.php?media=wiki:latex:/img4df44cc3ca1402586656741e233f0eb8.png)
- taking its transitive closure: computes all terms reachable by reduction
Non-termination and Difficulties with Semantics
Let  denote term
denote term
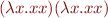
Note that  beta reduces to itself. It represents infinite loop.
beta reduces to itself. It represents infinite loop.
Note that the set of total functions is not a model of untyped lambda calculus. Consider the self-application expression  . Suppose the interpretation of variable
. Suppose the interpretation of variable  ranges over a domain
ranges over a domain  . This domain should be a set of total functions
. This domain should be a set of total functions  to enable application. But all possible values of
to enable application. But all possible values of  are an argument, so we have that
are an argument, so we have that
![Equation \begin{equation*}
D = [D \to D]
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img6a00baa06f3fe43eab84246e52c75b54.png)
that is, the set  is equal to the set of all functions from
is equal to the set of all functions from  to
to  . But this is not possible in set theory, because we can prove that the set
. But this is not possible in set theory, because we can prove that the set  has larger cardinality (even if it is infinite). For example, if
has larger cardinality (even if it is infinite). For example, if  is the set of natural numbers (which is countably infinite), then
is the set of natural numbers (which is countably infinite), then  would be uncountably infinite.
would be uncountably infinite.
The models of untyped lambda calculus do exist, but they usually consider only certain 'continuous', partial, functions. These domains are studied in domain theory. Roughly speaking, in domain theory, a solution to equation such as ![Math $D \simeq [D \leadsto D]$](/w/lib/exe/fetch.php?media=wiki:latex:/img13343c44a8862a78003189c05e5d1aeb.png) is obtained by finding a fixpoint of a monotonic operator
is obtained by finding a fixpoint of a monotonic operator ![Math $F(D) = [D \leadsto D]$](/w/lib/exe/fetch.php?media=wiki:latex:/img41e3bb9a080683b88aa3dfbc0508b501.png) .
.
Thus, untyped lambda calculus is easy to understand syntactically (as a set of rules for manipulating formal expressions), rather than a system where each expression has some intuitive meaning.
References:
- Barendregt, H. P. The Lambda Calculus: Its Syntax and Semantics. North Holland, Amsterdam (1984)