Better Backward Analysis
Like Safety checking of machine code, we base ourselves on boolean formulas over (linear) inequalities. This is why we need more than polyhedra:
package examples; import gov.nasa.jpf.rddsa.AbstrUtil; class PolyBad { static class A { public int f; public int g; } public static void main(String[] args) { A x = new A(); x.f = AbstrUtil.input(); if (x.f >= 6 ) { x.g = 2 * x.f; x.g = x.g - 2; } else { x.g = 3 * x.f; } AbstrUtil.Assert(x.g > 10); } }
Using one polyhedron, we have to obtain the convex hull between the two branches of the if, thus losing all the information inside. If we allow for arbitrary boolean expressions, then we can stay path-dependent. Another example is Unsafe module.
The language of the formulas
 | ::= | 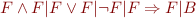 |
 | ::= | 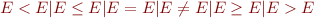 |
 | ::= | 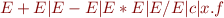 |
where 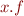 is field
is field  of variable
of variable  .
.
The analysis lattice
We work with the lattice of boolean formulas, with  being false and
being false and  being true. Join
being true. Join  is
is  ,
meet
,
meet  is
is  . Thus,
. Thus, 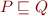 iff
iff  .
.
The error condition after the instruction is always taken to be  . For assert, we have to deal with the
. For assert, we have to deal with the
| Instruction | Abstract Interpretation |
|---|---|
![Math $[P]$](/w/lib/exe/fetch.php?media=wiki:latex:/img9349485c33bd3fbbf21dd478def7c254.png) | 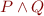 |
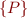 |  |
 | ![Math $Q[ x.f \rightarrow E]$](/w/lib/exe/fetch.php?media=wiki:latex:/img87ff1e17cb8694aac5731d75d4548b22.png) |
 | 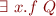 |
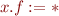 | 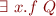 |
 | 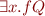 for every field for every field  of of  |
 | ![Math $Q[ x.f \rightarrow y.f \forall f \in fields(y)]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgd9fdfac2eb21923a71df8c0f8dd6b972.png) |
 | false |
Induction-iteration with error conditions
Calculating error conditions for non-looping code is feasible with these rules. However, as soon as we encounter loops, our error condition might grow indefinitely. This is where the induction-iteration method is used. We adapt it to deal with error conditions as follows:
- Let
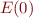 be the error condition obtained from going through the loop once back to the loop head and define
be the error condition obtained from going through the loop once back to the loop head and define  as going through the loop once more with the error condition
as going through the loop once more with the error condition 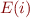 .
. - The error condition of the loop is
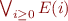
- Let

If we find an 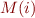 that is
that is
- False on entry of the loop
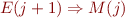
Then we have found an error condition that holds through the loop.
Report
The current report can be found here: Constant propagation and backward analysis.
SVN repository: https://svn.epfl.ch/svn/rddsa
Examples
The examples can be found in the svn repository under the directory trunk/javapathfinder/extensions/rddsa/src/examples . They are written in Java and can be run with the script run_example.sh . The CFG in the intermediary language that we are treating can be obtained by using doc/make_graph.sh .
Status
- I have all the infrastructure set up to obtain the intermediary language from Java bytecode and current state from JPF.
- I have written examples that could benefit from analysis in the middle of program execution
- I formulated the better backward analysis and tried it on some examples by hand
- The implementation of this backward analysis is not complete yet
Introduction
The current execution state of a program contains a lot of useful information about future program execution. This information could be used to better determine absence of certain errors and garbage collection information. An iterative analysis, running in parallel with program execution could obtain this information. I show how to combine the results of an iterative forward and backward analysis with current program state and use that information to detect absence of errors.
- Create CFG
- Run expensive backward analysis for some time
- At some point, run the state-dependent forward analysis. From the two analyses, see whether we can discharge assertions.
- All the time in parallel, continue running program
Using a forward analysis with symbolic objects per instantiation point and a complex backward analysis, I want to assure that the program does not run into an error in the future.
Motivating example
class Example { static class A { int f; int g; } public static void main(String[] args) { Random r = new Random(); A x = new A(); x.f = Integer.valueOf(args[0]); x.g = r.nextInt(); A y = new A(); TM(x,y); while (x.f != 1) { if (x.f % 2 == 0) x.f = x.f / 2; else x.f := x.f * 3 + 1; } assert x.g == y.g; } }
Where TM is a sufficiently complex procedure.
Incremental Analysis
Here is the current description of all the parts of the analysis tying in together: Constant propagation and backward analysis. There are, however, severe limitations to applicability.
- Define language of statement, transfer CFG
- For loops, we need some sort of integer manipulation if we only have one-level heap, otherwise it gets boring
- Define forward constant propagation and its use to discharge assertions
- At the moment, use the same abstraction of one store per instantiation point
- Can we do this iteratively, giving better results each step?
- define backward analysis
- Possibly better / more useful approach: Program Analysis as Constraint Solving
- Also related: Precise interprocedural analysis through linear algebra
- This one can be quite precise, as we are allowed to spend more time doing it (in parallel with program execution).
- We have to be able to merge results from forward and backward analysis to discharge assertions.
- see how we can combine the two
- Constant propagation results can be reused partially: If we have a concrete value for a field, it will really stay that way. Using this additional information, we can get a more precise error space.
Parallel, iterated execution
- Run one phase of backward analysis before program execution
- Update thread (to be run in parallel, separate core if possible):
- on fixed intervals, take the current program state and do a constant propagation
- if, during this execution we obtain an abstract state
 old state (i.e. more constants present) and we are at an instruction of the form x.f := *, recalculate this instruction replacing fields whose values are known with their constant value.
old state (i.e. more constants present) and we are at an instruction of the form x.f := *, recalculate this instruction replacing fields whose values are known with their constant value. - iterate the backward analysis until it converges again
- What happens if we are inside a loop?
Relevant
- Combining Shape Analyses by Intersecting Abstractions Sagiv et al. Using the TVLA framework, they show how they can combine information obtained by forward and backward analysis by calculating meet correspondences between structures.
- Weakest-Precondition of Unstructured Programs They do multiple transformations to source program (passivication etc.) that are then difficult to translate back to formulas having to hold at specific instructions
More, less related stuff: